《2025年新课标同步单元练习八年级数学下册北师大版深圳专版》

2. 如图1-2-9，用纸板挡住直角三角形一部分后，也能画出与此直角三角形全等的三角形，其依据是( )．


A. ASA
B. AAS
C. SAS
D. HL

答案： A

3. 如图1-2-10，在平面直角坐标系中，点$A(-2,0)$，$B(2,0)$，点$C$从点$O$出发，在第一象限内沿射线$y = \sqrt{3}x(x\geqslant0)$运动，当$\triangle ABC$是直角三角形时，点$C$的坐标为______．

答案： （1，$\sqrt{3}$）或（2，2$\sqrt{3}$）

4. 如图1-2-11，折叠长方形纸片$ABCD$，使点$D$落在边$BC$上的点$F$处，折痕为$AE$．已知$AB = 6\ cm$，$BC = 10\ cm$，则$EC$的长为______ $cm$．

答案： 8/3

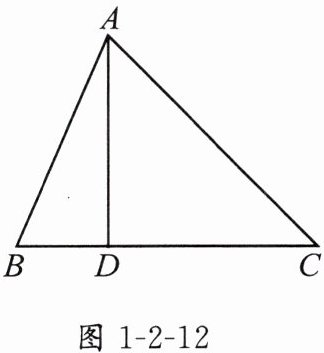
5. 如图1-2-12，在$\triangle ABC$中，$\angle ACB = 45^{\circ}$，$AD\perp BC$于点$D$．
(1)请用尺规按下列要求作图：以点$D$为圆心，$BD$长为半径画弧，交线段$AD$于点$E$，连接$CE$，并求证：$\triangle ABD\cong\triangle CED$；
(2)在(1)的条件下，若$CE$是$\angle ACD$的平分线，求$\angle BAC$的度数．

答案：
解：（1）尺规作图如答图1 - 2 - 2. 证明：因为AD⊥BC，∠ACB = 45°， 所以∠ADB = ∠CDE = 90°，△ADC是等腰直角三角形， 所以AD = CD， 在△ABD和△CED中， 所以△ABD≌△CED（SAS）.
（2）因为CE为∠ACD的平分线， 所以∠ECD = 1/2∠ACD = 22.5°. 由（1）得△ABD≌△CED， 所以∠BAD = ∠ECD = 22.5°. 所以∠BAC = ∠BAD + ∠CAD = 22.5° + 45° = 67.5°.

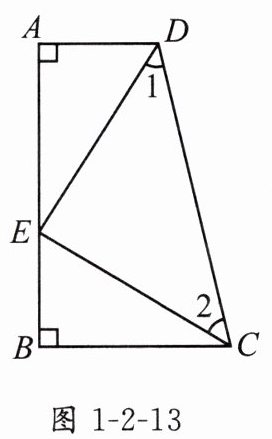
6. 如图1-2-13，$\angle A=\angle B = 90^{\circ}$，$E$是$AB$上的一点，且$AE = BC$，$\angle 1=\angle 2$．
(1)求证：$\triangle ADE\cong\triangle BEC$；
(2)请写出线段$CD$与$AD$，$BC$之间的数量关系，并说明理由．

答案：
（1）证明：因为∠1 = ∠2， 所以ED = EC. 在Rt△ADE和Rt△BEC中，

所以Rt△ADE≌Rt△BEC（HL）.
（2）解：AD² + BC² = 1/2CD². 理由：由（1）得Rt△ADE≌Rt△BEC，DE = CE， 所以∠AED = ∠BCE，BC = AE. 因为∠A = ∠B = 90°， 所以∠BCE + ∠CEB = 90°， 所以∠AED + ∠CEB = 90°， 所以∠DEC = 180° - 90° = 90°. 因为∠1 = ∠2， 所以△DEC为等腰直角三角形. 在Rt△ADE中，DE² = AD² + AE² = AD² + BC²， 在Rt△EDC中，CD² = DE² + CE² = 2DE² = 2（AD² + BC²）， 所以AD² + BC² = 1/2CD².