《2025年新课标同步单元练习八年级数学下册北师大版深圳专版》

4. 一块直角三角尺放在两平行直线上，如图1-2-2，则∠1 + ∠2 = ______°.

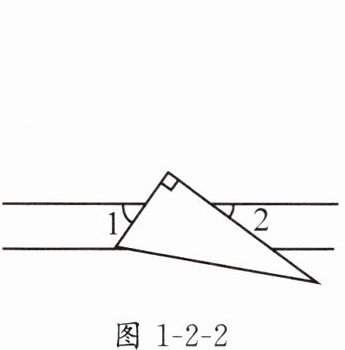
答案： 90

5. 如图1-2-3，已知钓鱼竿AC的长为10 m，露在水面上的鱼线BC长为6 m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC转动到AC′的位置，此时露在水面上的鱼线B′C′长为8 m，则BB′的长为_______m．

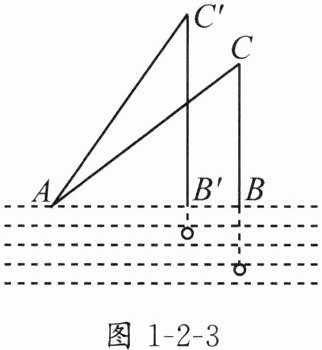
答案： 2

6. 如图1-2-4，一块铁皮(图中阴影部分)，测得AB = 3，BC = 4，CD = 12，AD = 13，∠B = 90°. 求阴影部分的面积．

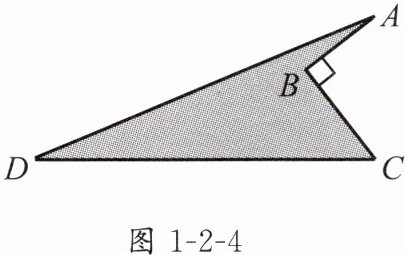
答案：
解：如答图1 - 2 - 1，连接AC. 因为△ABC中，∠B = 90°，AB = 3，BC = 4， 所以AC = $\sqrt{3² + 4²}$ = 5. 因为CD = 12，AD = 13，AC = 5， 所以AC² + CD² = AD²， 所以△ACD是直角三角形， 所以$S阴影$ = $S_{△ACD}$ - $S_{△ABC}$ = 1/2 × 5 × 12 - 1/2 × 3 × 4 = 30 - 6 = 24.

7. 如图1-2-5，在△ABC中，AB = AC，△ABC的高BH，CM交于点P．
(1)求证：PB = PC；
(2)若PB = 5，PH = 3，求AB的长．

答案： （1）证明：因为AB = AC， 所以∠ABC = ∠ACB. 因为BH，CM为△ABC的高， 所以∠BMC = ∠CHB = 90°. 所以∠ABC + ∠BCM = 90°，∠ACB + ∠CBH = 90°. 所以∠BCM = ∠CBH. 所以PB = PC. （2）解：因为PB = PC，PB = 5， 所以PC = 5. 因为PH = 3，∠CHP = 90°， 所以CH = 4. 设AB = x，则AH = x - 4. 在Rt△ABH中， 因为AH² + BH² = AB²， 所以(x - 4)² + (5 + 3)² = x². 所以x = 10， 即AB = 10.