第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
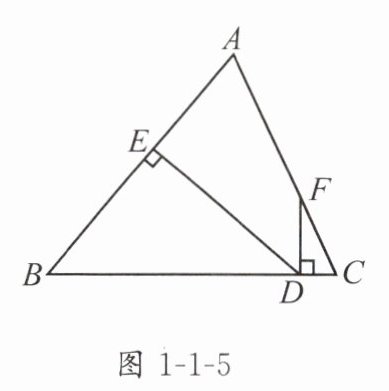
7. 如图1-1-5,在$\triangle ABC$中,$AB = BC$,$D$为$BC$上一点,作$DE\perp AB$于点$E$,作$DF\perp BC$于点$D$,交$AC$于点$F$.
(1)若$\angle AFD = 155^{\circ}$,求$\angle EDF$的度数;
(2)若点$F$是$AC$的中点,求证:$\angle CFD=\frac{1}{2}\angle B$.
(1)若$\angle AFD = 155^{\circ}$,求$\angle EDF$的度数;
(2)若点$F$是$AC$的中点,求证:$\angle CFD=\frac{1}{2}\angle B$.

答案:
(1)解:因为∠AFD = 155°, 所以∠DFC = 25°. 因为DF⊥BC,DE⊥AB, 所以∠FDC = ∠AED = 90°. 在Rt△FDC中, ∠C = 90° - 25° = 65°. 因为AB = BC, 所以∠A = ∠C = 65°, 所以∠EDF = 360° - 65° - 155° - 90° = 50°.
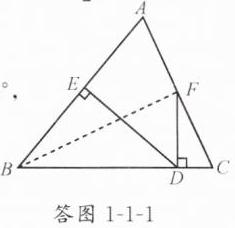
(2)证明:如答图1 - 1 - 1,连接BF. 因为AB = BC,且点F是AC的中点, 所以BF⊥AC,∠ABF = ∠CBF = 1/2∠ABC, 所以∠CFD + ∠BFD = 90°. 又因为∠CBF + ∠BFD = 90°, 所以∠CFD = ∠CBF, 所以∠CFD = 1/2∠ABC.
(1)解:因为∠AFD = 155°, 所以∠DFC = 25°. 因为DF⊥BC,DE⊥AB, 所以∠FDC = ∠AED = 90°. 在Rt△FDC中, ∠C = 90° - 25° = 65°. 因为AB = BC, 所以∠A = ∠C = 65°, 所以∠EDF = 360° - 65° - 155° - 90° = 50°.
(2)证明:如答图1 - 1 - 1,连接BF. 因为AB = BC,且点F是AC的中点, 所以BF⊥AC,∠ABF = ∠CBF = 1/2∠ABC, 所以∠CFD + ∠BFD = 90°. 又因为∠CBF + ∠BFD = 90°, 所以∠CFD = ∠CBF, 所以∠CFD = 1/2∠ABC.

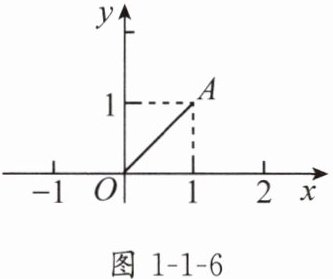
1. 如图1-1-6,点$A$的坐标是$(1,1)$,若点$B$在$x$轴上,且$\triangle ABO$是等腰三角形,则点$B$的坐标可能是______.

答案:
(− $\sqrt{2}$ ,0),( $\sqrt{2}$ ,0),(1,0),(2,0)
2. 如图1-1-7,在$\triangle ABC$中,$AB = 3\ cm$,$AC = 4\ cm$,$BC = 5\ cm$,过$\triangle ABC$的顶点画一条直线,将$\triangle ABC$分割成两个三角形,使其中的一个是等腰三角形,这样的直线最多可画______条.


答案:
6
3. 我们经常遇到需要分类的问题,画“树形图”可以帮我们不重复、不遗漏地分类.
【例题】
在等腰三角形$ABC$中,若$\angle A = 80^{\circ}$,求$\angle B$的度数.
分析:$\angle A$,$\angle B$都可能是顶角或底角,因此需要分成如图1-1-8所示的3类,这样的图就是树形图,据此可求出$\angle B = 50^{\circ}$或$\angle B = 80^{\circ}$或$\angle B = 20^{\circ}$.
分类$\begin{cases}\angle A为顶角——\angle B为底角\\\angle A为底角\begin{cases}\angle B为底角\\\angle B为顶角\end{cases}\end{cases}$
图1-1-8
【应用】
(1)已知等腰三角形$ABC$的周长为19,$AB = 7$,仿照例题画出树形图,并直接写出$BC$的长度;
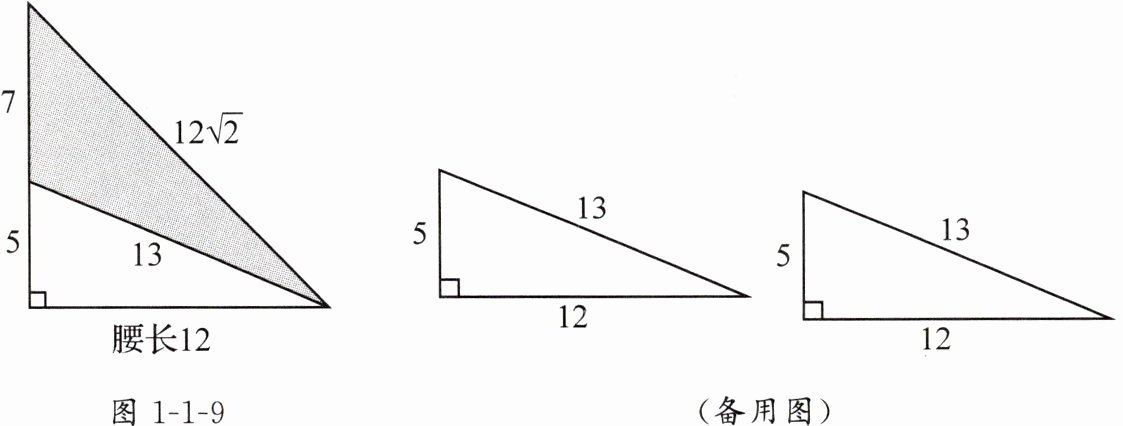
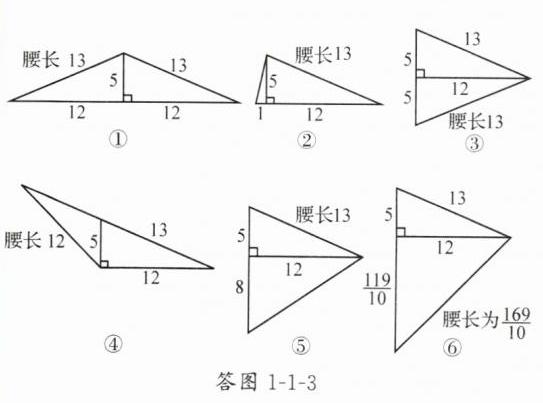
(2)将一个边长分别为5,12,13的直角三角形拼上一个三角形后可以拼成一个等腰三角形,图1-1-9就是其中的一种拼法,请你画出其他所有可能的情形,并在图上标出所拼成等腰三角形的腰的长度.(选用备用图画图,每种情形用一个图形单独表示,并用①②③…编号,若备用图不够,请自己画图补充)
【例题】
在等腰三角形$ABC$中,若$\angle A = 80^{\circ}$,求$\angle B$的度数.
分析:$\angle A$,$\angle B$都可能是顶角或底角,因此需要分成如图1-1-8所示的3类,这样的图就是树形图,据此可求出$\angle B = 50^{\circ}$或$\angle B = 80^{\circ}$或$\angle B = 20^{\circ}$.
分类$\begin{cases}\angle A为顶角——\angle B为底角\\\angle A为底角\begin{cases}\angle B为底角\\\angle B为顶角\end{cases}\end{cases}$
图1-1-8
【应用】
(1)已知等腰三角形$ABC$的周长为19,$AB = 7$,仿照例题画出树形图,并直接写出$BC$的长度;
(2)将一个边长分别为5,12,13的直角三角形拼上一个三角形后可以拼成一个等腰三角形,图1-1-9就是其中的一种拼法,请你画出其他所有可能的情形,并在图上标出所拼成等腰三角形的腰的长度.(选用备用图画图,每种情形用一个图形单独表示,并用①②③…编号,若备用图不够,请自己画图补充)

答案:
解:
(1)树形图如答图1 - 1 - 2:
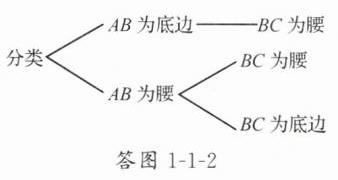
当AB为底边,BC为腰时,BC = 1/2×(19 - 7)=6; 当AB为腰,BC为腰时,BC = AB = 7; 当AB为腰,BC为底边时,BC = 19 - 2×7 = 5. 经检验,上述三种情况均符合题意. 综上所述,BC的长度是5,6或7.
(2)如答图1 - 1 - 3,共有6种情形.
解:
(1)树形图如答图1 - 1 - 2:

当AB为底边,BC为腰时,BC = 1/2×(19 - 7)=6; 当AB为腰,BC为腰时,BC = AB = 7; 当AB为腰,BC为底边时,BC = 19 - 2×7 = 5. 经检验,上述三种情况均符合题意. 综上所述,BC的长度是5,6或7.
(2)如答图1 - 1 - 3,共有6种情形.

查看更多完整答案,请扫码查看


