《2025年新课程学习与检测九年级数学上册》

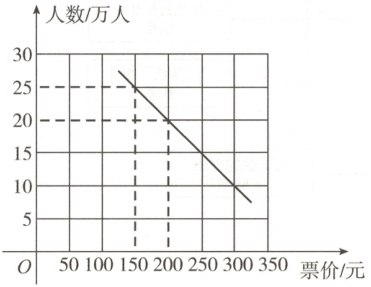
8. 某景区采取了涨门票价格的方法来控制旅游人数，在该方法实施过程中发现：每周旅游人数与票价之间存在着如图所示的一次函数关系. 在这种情况下，如果要保证每周 3000 万元的门票收入，那么每周应限定旅游人数多少人？门票价格应是多少元？

答案： 8.解：设每周旅游人数与票价之间的一次函数
关系式为y=kx+b，
把(150,25)，(200,20)的坐标代入y=kx+
b中，得$\begin{cases}150k+b=25,\\200k+b=20,\end{cases}$
解得$\begin{cases}k=-0.1,\\b=40,\end{cases}$
所以y=-0.1x+40.
因为要保证每周3000万元的门票收入，
所以xy=3000，
即x(-0.1x+40)=3000，
$x^{2}-400x+30000=0，$
解得$x_{1}=100，$$x_{2}=300.$
把$x_{1}=100，$$x_{2}=300$分别代入y=-0.1x+40
中，得$y_{1}=30，$$y_{2}=10.$
因为控制旅游人数，所以取x=300，y=10.
答：每周应限定旅游人数为10万人，门票价
格应是300元/人.

9. 某种新产品的进价是 120 元，在试销阶段发现，每件销售价格(元)与产品的日销售量(件)始终存在下表中的数量关系.

(1)请你观察上面表格中数据的变化规律，回答：当每件产品每涨价 1 元时，日销售量是怎样变化的？
(2)在不改变上述关系的情况下，请你帮助商场经理策划：每件产品的定价为多少元，可使每日盈利达到 1600 元.

答案： 9.解：
(1)
∵130+70=200，135+65=200，
140+60=200，
∴每件的销售价格与产品的日销售量之和
为200.
∴当每件产品每涨价1元时，日销售量减少
1件.
(2)设每件产品定价为x元(x＞120)，则产
品的日销售量为(200-x)件，
由题意得(x-120)(200-x)=1600，
整理得$x^{2}-320x+25600=0，$
解得$x_{1}=x_{2}=160.$
答：每件产品定价为160元时，可使每日盈
利达到1600元.