《2025年新课程学习与检测九年级数学上册》

6. 一片小小的树叶也蕴含着“黄金分割”的美。如图所示，P为线段AB的黄金分割点$(AP＞PB)$。如果AB的长度为10cm，那么AP的长度是(A)


A.$(5\sqrt{5}-5)$cm
B.$(15-5\sqrt{5})$cm
C.6.18cm
D.$(5\sqrt{5}+5)$cm

答案： 6.A

7. 大自然是美的设计师，即使是一个小小的盆景，也会产生最具美感的黄金分割比(黄金分割比$=\frac{\sqrt{5}-1}{2}$)。如图所示，B为AC的黄金分割点$(AB＞BC)$，若$AC=20$cm，则BC的长为$(30 - 10\sqrt{5})$cm。(结果保留根号)

答案： 7.$(30 - 10\sqrt{5})$

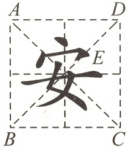
8. 如图所示，这是“安”字在正方形米字格中的书写形态，已知正方形ABCD的边长为2cm，笔画横钩“乛”与正方形的对角线交于点E，点E为线段BD的黄金分割点，$DE＜BE$，则DE的长为$(3\sqrt{2} - \sqrt{10})$cm。(结果保留根号)

答案： 8.$(3\sqrt{2} - \sqrt{10})$

9. 古今中外，人们把黄金分割誉为“天赋”的比例法则，它是几何学中一大瑰宝。
(1)如图1所示，若$AB=10$，点H是线段AB的黄金分割点$(AH＞BH)$，求线段AH的长。
(2)如图2所示，在$\triangle ABC$中，$AB=AC$，$∠A=36^{\circ}$，CM是$∠ACB$的平分线，求证：点M是线段AB的黄金分割点。

答案： 9.
(1)解：$\because$点$H$是线段$AB$的黄金分割点$(AH ＞ BH)$，$\therefore\frac{AH}{AB}=\frac{\sqrt{5}-1}{2}$．
又$\because AB = 10$，$\therefore AH = 5\sqrt{5}-5$．
(2)证明：$\because AB = AC$，$\angle A = 36^{\circ}$，
$\therefore\angle ABC = \angle ACB = 72^{\circ}$．
$\because CM$平分$\angle ACB$，
$\therefore\angle ACM = \angle BCM = 36^{\circ}$．
$\therefore\angle A = \angle ACM$．$\therefore AM = MC$．
又$\because\angle BMC = \angle A + \angle ACM = 72^{\circ}$，
$\therefore\angle BMC = \angle ABC$．
$\therefore BC = MC$．$\therefore BC = AM$．
$\because\angle A = \angle BCM$，$\angle B = \angle B$，
$\therefore\triangle ABC\sim\triangle CBM$．
$\because\frac{BM}{BC}=\frac{BC}{AB}$．
$\therefore\frac{BM}{AM}=\frac{AM}{AB}$．
$\therefore$点$M$是线段$AB$的黄金分割点．

1. 如图所示，在矩形 $ABCD$ 中，$E$ 是 $AD$ 的中点，$F$ 是 $CD$ 上一点，连接 $BE$，$BF$，$EF$。若 $\angle BEF = 90^{\circ}$，

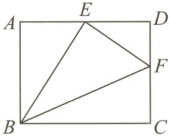
$\frac{EF}{BE} = \frac{2}{3}$，则 $\frac{CF}{DF}$ 的值为(D)

A.$\frac{\sqrt{5}}{2}$
B.$\frac{3}{2}$
C.$\frac{4}{3}$
D.$\frac{5}{4}$

答案： 1.D