2025年人教金学典同步练习册同步解析与测评高中数学选择性必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年人教金学典同步练习册同步解析与测评高中数学选择性必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
例 已知一艘海监船上配有雷达,雷达的监测范围是半径为 $ 50 $ n mile 的圆形区域,一艘轮船从位于海监船正东 $ 80 $ n mile 的 $ A $ 港口出发,径直驶向位于海监船正北 $ 60 $ n mile 的 $ B $ 岛屿,航行速度为 $ 28 $ n mile/h. 这艘轮船能否被海监船监测到? 若能,监测的时间持续多长?
答案:
分析:先依据题意画出方位图(如图 2.5 - 2,记海监船位置为 $ O $),通过建立适当的平面直角坐标系,求出轮船航线所在的直线方程,以及圆心到直线的距离,从而可确定直线和圆的位置关系,由此可以解决问题.
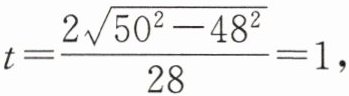
解:记海监船位置为 $ O $. 如图 2.5 - 2,以点 $ O $ 为原点,海监船的正东方向为 $ x $ 轴的正方向,正北方向为 $ y $ 轴的正方向建立平面直角坐标系(1 个单位长度代表 $ 10 $ nmile),则 $ A(80, 0) $,$ B(0, 60) $,圆 $ O $ 的方程为 $ x^2 + y^2 = 2500 $,直线 $ AB $ 的方程为 $ \frac{x}{80} + \frac{y}{60} = 1 $,即 $ 3x + 4y - 240 = 0 $.
点 $ O $ 到直线 $ AB $ 的距离 $ d = \frac{240}{5} = 48 $.
因为 $ d = 48 < 50 $,所以海监船能监测到轮船.
当这艘轮船经过 $ CD $ 航段时,能被海监船监测到.
因为 $ CD = 2\sqrt{OC^2 - d^2} = 2\sqrt{50^2 - 48^2} $,所以监测持续的时间
$ t = \frac{2\sqrt{50^2 - 48^2}}{28} = 1 $,
即监测时间持续 $ 1 $ h.
评析:本题为实际问题,通过建立平面直角坐标系,运用坐标法将其转化为直线与圆的位置关系问题,通过研究直线与圆的位置关系可得到实际问题的结果.

分析:先依据题意画出方位图(如图 2.5 - 2,记海监船位置为 $ O $),通过建立适当的平面直角坐标系,求出轮船航线所在的直线方程,以及圆心到直线的距离,从而可确定直线和圆的位置关系,由此可以解决问题.
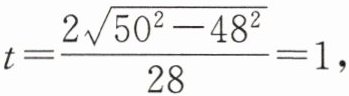
解:记海监船位置为 $ O $. 如图 2.5 - 2,以点 $ O $ 为原点,海监船的正东方向为 $ x $ 轴的正方向,正北方向为 $ y $ 轴的正方向建立平面直角坐标系(1 个单位长度代表 $ 10 $ nmile),则 $ A(80, 0) $,$ B(0, 60) $,圆 $ O $ 的方程为 $ x^2 + y^2 = 2500 $,直线 $ AB $ 的方程为 $ \frac{x}{80} + \frac{y}{60} = 1 $,即 $ 3x + 4y - 240 = 0 $.
点 $ O $ 到直线 $ AB $ 的距离 $ d = \frac{240}{5} = 48 $.
因为 $ d = 48 < 50 $,所以海监船能监测到轮船.
当这艘轮船经过 $ CD $ 航段时,能被海监船监测到.
因为 $ CD = 2\sqrt{OC^2 - d^2} = 2\sqrt{50^2 - 48^2} $,所以监测持续的时间
$ t = \frac{2\sqrt{50^2 - 48^2}}{28} = 1 $,
即监测时间持续 $ 1 $ h.
评析:本题为实际问题,通过建立平面直角坐标系,运用坐标法将其转化为直线与圆的位置关系问题,通过研究直线与圆的位置关系可得到实际问题的结果.

1. 一辆卡车宽 $ 1.6 $ m,要经过一个半圆形隧道口(半径为 $ 3.6 $ m),则这辆卡车的平顶车篷的篷顶距地面的高度不得超过( ).
A.$ 1.4 $ m
B.$ 3.5 $ m
C.$ 3.6 $ m
D.$ 2.0 $ m
A.$ 1.4 $ m
B.$ 3.5 $ m
C.$ 3.6 $ m
D.$ 2.0 $ m
答案:
1. B
[解析]画出示意图,如图,$OB = 0.8m$,$OA = 3.6m$。在$Rt\triangle AOB$中,根据勾股定理得$AB=\sqrt{OA^{2}-OB^{2}}\approx3.5(m)$,则这辆卡车的篷顶距地面的高度不得超过$3.5m$。

1. B
[解析]画出示意图,如图,$OB = 0.8m$,$OA = 3.6m$。在$Rt\triangle AOB$中,根据勾股定理得$AB=\sqrt{OA^{2}-OB^{2}}\approx3.5(m)$,则这辆卡车的篷顶距地面的高度不得超过$3.5m$。

2. 台风中心从 $ A $ 地以 $ 20 $ km/h 的速度向东北方向移动,离台风中心 $ 30 $ km 内的地区为危险地区. 若城市 $ B $ 在 $ A $ 地正东 $ 40 $ km 处,则城市 $ B $ 处于危险区的时间为( ).
A.$ 0.5 $ h
B.$ 1 $ h
C.$ 1.5 $ h
D.$ 2 $ h
A.$ 0.5 $ h
B.$ 1 $ h
C.$ 1.5 $ h
D.$ 2 $ h
答案:
2. B
[解析]以$A$为原点,建立如图所示的平面直角坐标系,则$B(40,0)$,台风中心移动的轨迹为射线$y = x(x\geq0)$,
而点$B$到射线$y = x$的距离$d=\frac{40}{\sqrt{2}}=20\sqrt{2}(km)<30(km)$,
故$l = 2\sqrt{30^{2}-(20\sqrt{2})^{2}}=20(km)$。故$B$城市处于危险区内的时间为$1h$。

2. B
[解析]以$A$为原点,建立如图所示的平面直角坐标系,则$B(40,0)$,台风中心移动的轨迹为射线$y = x(x\geq0)$,
而点$B$到射线$y = x$的距离$d=\frac{40}{\sqrt{2}}=20\sqrt{2}(km)<30(km)$,
故$l = 2\sqrt{30^{2}-(20\sqrt{2})^{2}}=20(km)$。故$B$城市处于危险区内的时间为$1h$。

3. $ A $,$ B $ 两地都出售同一种大型商品,且价格相同,但从两地购得商品后运回的费用不同,从 $ A $ 地运回商品每千米的运费是从 $ B $ 地运回商品每千米的运费的 $ 3 $ 倍. 已知 $ A $,$ B $ 两地相距 $ 10 $ km,顾客选择 $ A $ 地或 $ B $ 地购买这种商品的标准为在何地购买的总费用(包括运费和价格因素)更低. 探究 $ A $,$ B $ 两地的售货区域的分界线的曲线形状,并分别指出曲线上、曲线内、曲线外的顾客应该如何选择购货地.
答案:
3. 如图,以$A$,$B$所在的直线为$x$轴,线段$AB$的中点为原点,建立平面直角坐标系,因为$\vert AB\vert = 10$,所以$A(-5,0)$,$B(5,0)$。

设点$P(x,y)$,设点$P$到$B$地购物的运费是$a$(元/km),则点$P$到$A$地购物的运费为$3a$(元/km)。
当点$P$到$A$,$B$两地购物总费用相等时,得$3a\sqrt{(x + 5)^{2}+y^{2}}=a\sqrt{(x - 5)^{2}+y^{2}}$,化简整理,得$(x+\frac{25}{4})^{2}+y^{2}=(\frac{15}{4})^{2}$。
故$A$,$B$两地的售货区域的分界线的形状为以$C(-\frac{25}{4},0)$为圆心,$\frac{15}{4}$为半径的圆。故在圆$C$内的居民从$A$地购物便宜,圆$C$外的居民从$B$地购物便宜,圆$C$上的居民从$A$,$B$两地购物的费用相等,可任意选择。
3. 如图,以$A$,$B$所在的直线为$x$轴,线段$AB$的中点为原点,建立平面直角坐标系,因为$\vert AB\vert = 10$,所以$A(-5,0)$,$B(5,0)$。

设点$P(x,y)$,设点$P$到$B$地购物的运费是$a$(元/km),则点$P$到$A$地购物的运费为$3a$(元/km)。
当点$P$到$A$,$B$两地购物总费用相等时,得$3a\sqrt{(x + 5)^{2}+y^{2}}=a\sqrt{(x - 5)^{2}+y^{2}}$,化简整理,得$(x+\frac{25}{4})^{2}+y^{2}=(\frac{15}{4})^{2}$。
故$A$,$B$两地的售货区域的分界线的形状为以$C(-\frac{25}{4},0)$为圆心,$\frac{15}{4}$为半径的圆。故在圆$C$内的居民从$A$地购物便宜,圆$C$外的居民从$B$地购物便宜,圆$C$上的居民从$A$,$B$两地购物的费用相等,可任意选择。
查看更多完整答案,请扫码查看


