《2025年人教金学典同步练习册同步解析与测评高中数学选择性必修第一册人教版》

1. 下列命题中正确的是（ ）.

A.若 $ |\boldsymbol{a}| = |\boldsymbol{b}| $，则 $ \boldsymbol{a} = \boldsymbol{b} $
B.若异面直线 $ l_1 $，$ l_2 $ 的方向向量分别为 $ \boldsymbol{a} $，$ \boldsymbol{b} $，则向量 $ \boldsymbol{a} $，$ \boldsymbol{b} $ 一定不共面
C.$ \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = \overrightarrow{AB} + \overrightarrow{CD} + \overrightarrow{BC} $
D.若 $ m \boldsymbol{a} = m \boldsymbol{b} $（$ m \in \mathbf{R} $），则 $ \boldsymbol{a} = \boldsymbol{b} $

答案： 1.C
【解析】对于A选项，两向量的模相等，方向不一定相同，故A选项错误；对于B选项，向量是可以平移的，故B选项错误；对于C选项，根据向量的交换律可知其正确；对于D选项，当m=0时不成立，故D选项错误.

2. 在三棱锥 $ S - ABC $ 中，$ \overrightarrow{SA} = \boldsymbol{a} $，$ \overrightarrow{SB} = \boldsymbol{b} $，$ \overrightarrow{SC} = \boldsymbol{c} $，$ D $ 为棱 $ BC $ 的中点，$ E $ 为线段 $ AD $ 的中点，则 $ \overrightarrow{SE} = $（ ）.

A.$ \frac{1}{2} \boldsymbol{a} + \frac{1}{4} \boldsymbol{b} + \frac{1}{4} \boldsymbol{c} $
B.$ \frac{1}{2} \boldsymbol{a} + \frac{1}{2} \boldsymbol{b} + \frac{1}{2} \boldsymbol{c} $
C.$ \frac{1}{4} \boldsymbol{a} + \frac{1}{4} \boldsymbol{b} + \frac{1}{4} \boldsymbol{c} $
D.$ \frac{1}{2} \boldsymbol{a} - \frac{1}{4} \boldsymbol{b} + \frac{1}{4} \boldsymbol{c} $

答案： 2.A
【解析$】\overrightarrow{SE}=\overrightarrow{SA}+\overrightarrow{AE}=\overrightarrow{SA}+\frac{1}{2}\overrightarrow{AD}=\overrightarrow{SA}+\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})$
$=\overrightarrow{SA}+\frac{1}{4}(\overrightarrow{SB}-\overrightarrow{SA}+\overrightarrow{SC}-\overrightarrow{SA})$
$=\frac{1}{2}\overrightarrow{SA}+\frac{1}{4}\overrightarrow{SB}+\frac{1}{4}\overrightarrow{SC}$
$=\frac{1}{2}a+\frac{1}{4}b+\frac{1}{4}c.$

3. 已知 $ \boldsymbol{a} $，$ \boldsymbol{b} $，$ \boldsymbol{c} $ 是三个不共面的向量，$ \boldsymbol{m} = \boldsymbol{a} + \boldsymbol{b} + 2 \boldsymbol{c} $，$ \boldsymbol{n} = x \boldsymbol{a} + y \boldsymbol{b} + \boldsymbol{c} $，若 $ \boldsymbol{m} $ 与 $ \boldsymbol{n} $ 共线，则 $ x = $______，$ y = $______.

答案： $3.\frac{1}{2};\frac{1}{2}$
【解析】由题意可知$,\frac{1}{x}=\frac{1}{y}=\frac{2}{1},$所以$x=y=\frac{1}{2}.$

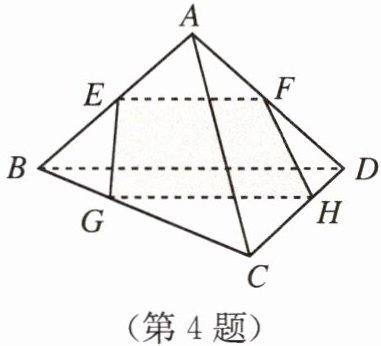
4. 如图，已知 $ E $，$ F $ 分别为四面体 $ ABCD $ 的棱 $ AB $，$ AD $ 的中点，$ \overrightarrow{BG} = \frac{1}{3} \overrightarrow{BC} $，$ \overrightarrow{DH} = \frac{1}{3} \overrightarrow{DC} $. 求证：$ E $，$ F $，$ G $，$ H $ 四点共面.

答案： 4.由E,F分别为棱AB,AD的中点,得$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{BD}.$
由$\overrightarrow{CG}=\frac{2}{3}\overrightarrow{CB},\overrightarrow{CH}=\frac{2}{3}\overrightarrow{CD},$得$\overrightarrow{GH}=\overrightarrow{CH}-\overrightarrow{CG}=\frac{2}{3}\overrightarrow{BD}.$所以$\overrightarrow{EF}=\frac{3}{4}\overrightarrow{GH},$从而$\overrightarrow{EF}//\overrightarrow{GH},$所以E,F,G,H四点共面.
方法总结
对空间四点P,M,A,B可通过证明下列结论成立来证明四点共面：
$(1)\overrightarrow{MP}=x\overrightarrow{MA}+y\overrightarrow{MB};$
(2)对空间任一点$O,\overrightarrow{OP}=x\overrightarrow{OM}+y\overrightarrow{MA}+y\overrightarrow{MB};$
(3)对空间任一点$O,\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}(x+y+z=1);$
$(4)\overrightarrow{PM}//\overrightarrow{AB}($或$\overrightarrow{PA}//\overrightarrow{MB},$或$\overrightarrow{PB}//\overrightarrow{AM}).$

1. 如图，在三棱柱 $ ABC - A_1 B_1 C_1 $ 中，$ \overrightarrow{AB} = \boldsymbol{a} $，$ \overrightarrow{AC} = \boldsymbol{b} $，$ \overrightarrow{AA_1} = \boldsymbol{c} $，$ D $ 为棱 $ CC_1 $ 的中点，$ \overrightarrow{A_1 E} = \frac{1}{3} \overrightarrow{A_1 B} $，则 $ \overrightarrow{DE} = $______（用向量 $ \boldsymbol{a} $，$ \boldsymbol{b} $，$ \boldsymbol{c} $ 表示）.

答案： $1.\frac{1}{3}a-b+\frac{1}{6}c$