第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
18. 如图,把两个面积均为$18 cm^2$的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.
(1) 大正方形纸片的边长为
(2) 若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长与宽之比为$4:3$,且面积为$24 cm^2$?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.
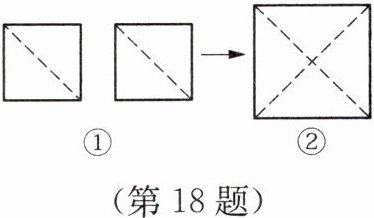
(1) 大正方形纸片的边长为
6
$ cm$.(2) 若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长与宽之比为$4:3$,且面积为$24 cm^2$?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.

能裁剪出.$\because$ 长方形纸片的长与宽之比为$4:3$,$\therefore$ 设长方形纸片的长和宽分别是$4x\ cm$、$3x\ cm$.$\therefore 3x\cdot4x=24$.$\therefore x^2=2$.$\because x>0$,$\therefore x=\sqrt{2}$.$\therefore$ 长方形纸片的长是$4x=4\sqrt{2}\ cm$,长方形纸片的宽是$3x=3\sqrt{2}\ cm$.$\because 4\sqrt{2}<6$,$\therefore$ 能裁剪出,剪出的长方形纸片的长是$4\sqrt{2}\ cm$,宽是$3\sqrt{2}\ cm$
答案:
(1)6 (2)能裁剪出.$\because$ 长方形纸片的长与宽之比为$4:3$,$\therefore$ 设长方形纸片的长和宽分别是$4x\ cm$、$3x\ cm$.$\therefore 3x\cdot4x=24$.$\therefore x^2=2$.$\because x>0$,$\therefore x=\sqrt{2}$.$\therefore$ 长方形纸片的长是$4x=4\sqrt{2}\ cm$,长方形纸片的宽是$3x=3\sqrt{2}\ cm$.$\because 4\sqrt{2}<6$,$\therefore$ 能裁剪出,剪出的长方形纸片的长是$4\sqrt{2}\ cm$,宽是$3\sqrt{2}\ cm$
1. (浙江中考) -8 的立方根是【
A.-2
B.2
C.±2
D.不存在
A
】A.-2
B.2
C.±2
D.不存在
答案:
A
2. 体积为 9 的立方体的棱长为【
A.$\sqrt[3]{9}$
B.$\sqrt[3]{3}$
C.$\sqrt{3}$
D.3
A
】A.$\sqrt[3]{9}$
B.$\sqrt[3]{3}$
C.$\sqrt{3}$
D.3
答案:
A
3. 下列语句中,正确的是【
A.$(-1)^2$ 的立方根是 -1
B.-3 是 27 的负的立方根
C.$\frac{125}{216}$ 的立方根是 $\pm\frac{5}{6}$
D.$\sqrt{64}$ 的立方根是 2
D
】A.$(-1)^2$ 的立方根是 -1
B.-3 是 27 的负的立方根
C.$\frac{125}{216}$ 的立方根是 $\pm\frac{5}{6}$
D.$\sqrt{64}$ 的立方根是 2
答案:
D
4. 如图,数轴上表示 $\sqrt[3]{27}+\sqrt[3]{-8}$ 的点一定在【
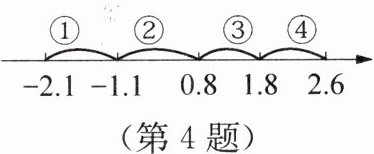
A.①段
B.②段
C.③段
D.④段
C
】
A.①段
B.②段
C.③段
D.④段
答案:
C
5. 利用计算器计算: $\sqrt{18}+\sqrt[3]{6}\approx$
6.06
. (精确到 0.01)
答案:
6.06
6. -8 的立方根与 4 的算术平方根的积为
-4
.
答案:
-4
查看更多完整答案,请扫码查看


