《2025年学习力提升九年级数学上册浙教版》

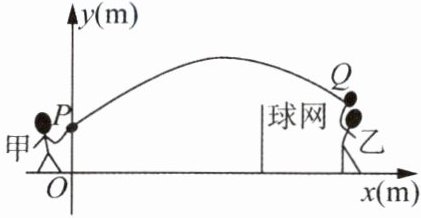
7. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在 $ O $ 点正上方 $ 1 $ m 的 $ P $ 处发出一球,羽毛球飞行的高度 $ y $(m)与水平距离 $ x $(m)之间满足函数表达式 $ y = -\frac{1}{24}(x - 4)^2 + h $,已知点 $ O $ 与球网的水平距离为 $ 5 $ m,球网的高度为 $ 1.55 $ m.
(1) 求 $ h $ 的值；
(2) 通过计算判断此球能否过网.

答案：
(1)将点P(0,1)代入$y=-\frac {1}{24}(x-4)^{2}+h$,得$-\frac {1}{24}×16+h=1$,解得$h=\frac {5}{3}(m).$
(2)把$x=5$代入$y=-\frac {1}{24}(x-4)^{2}+\frac {5}{3}$,得$y=-\frac {1}{24}(5-4)^{2}+\frac {5}{3}=1.625(m).$$\because 1.625m＞1.55m$,
∴此球能过网.

8. 某商店购进某种商品的价格是每件 2.5 元,在一段时间里,售出单价为 13.5 元时,销售量为 500 件,而销售单价每降低 3 元就可多售出 600 件. 当销售单价为每件 $ x $ 元时,所获利润为 $ y $ 元,那么 $ y $ 关于 $ x $ 的函数表达式为$y=-200x^{2}+3700x-8000(2.5≤x≤13.5)$.

答案： $y=-200x^{2}+3700x-8000(2.5≤x≤13.5)$

9. 某电器城准备销售一种型号的手机,在销售过程中发现,当零售价为每台 4000 元时,每天可以售出 8 台,日销售利润为 4000 元,当零售价每降低 50 元时,则每天多售出 4 台,下列结论正确的是(A)
A.当零售价降低 200 元时,日销售利润最大,最大利润为 7200 元
B.当零售价降低 100 元和零售价降低 300 元时,销售数量是一样的
C.手机的进价是每台 500 元
D.零售价越低,每天售出数量就越多,所以利润就越大

答案： 9.A 解析:A选项,设该型号手机的零售价降低x元,日销售利润为W元,$\therefore W=(\frac {4000}{8}-x)(8+\frac {x}{50}×4)=-\frac {2}{25}(x-200)^{2}+7200,$$\because a＜0$,
∴当$x=200$时,W最大为7200元,故A符合题意.B选项,当零售价降低100元时,销售量为:$8+100÷50×4=16$台，零售价降低300元时,销售量为:$8+300÷50×4=32$台，
∴当零售价降低100元和零售价降低300元时,销售数量是不一样的,故B不符合题意.C选项,
∵当零售价为每台4000元时,每天可以售出8台,日销售利润为4000元,
∴手机的进价为$4000-4000÷8=3500$元,故C不符合题意.D选项,零售价越低,每天售出数量就越多,利润不一定越大,故D不符合题意.故答案为:A.