第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
例1 (1)已知$a= -2$,求$5a^{2}-[3a-(2a-3)+4a^{2}]$的值;
(2)已知$a^{2}-ab= 8$,$ab-b^{2}= -4$,求$a^{2}-b^{2}和a^{2}-2ab+b^{2}$的值.
(2)已知$a^{2}-ab= 8$,$ab-b^{2}= -4$,求$a^{2}-b^{2}和a^{2}-2ab+b^{2}$的值.
答案:
解:
(1) 原式= 5a²-(3a-2a+3 + 4a²)
= 5a²-(a +3+ 4a²)
= 5a²-a-3-4a²
=a²-a- 3.
当a=-2时,原式= (-2)²-(-2)-3= 4+2-3= 3.
(2)因为a²-b²=a²-ab+ab-b²= (a²-ab)+(ab-b²),
所以把a²-ab= 8,ab-b²=-4代入,得a²-b²= (a²-ab)+(ab-b²)=8+(-4)=4.
因为a²- 2ab+b²=a²-ab-ab+b²= (a²-ab)-(ab-b²),
所以把a²-ab= 8,ab-b²=-4代入,得a²-2ab+b² = (a²-ab)- (ab-b²)=8-(-4) - 8+4= 12.
(1) 原式= 5a²-(3a-2a+3 + 4a²)
= 5a²-(a +3+ 4a²)
= 5a²-a-3-4a²
=a²-a- 3.
当a=-2时,原式= (-2)²-(-2)-3= 4+2-3= 3.
(2)因为a²-b²=a²-ab+ab-b²= (a²-ab)+(ab-b²),
所以把a²-ab= 8,ab-b²=-4代入,得a²-b²= (a²-ab)+(ab-b²)=8+(-4)=4.
因为a²- 2ab+b²=a²-ab-ab+b²= (a²-ab)-(ab-b²),
所以把a²-ab= 8,ab-b²=-4代入,得a²-2ab+b² = (a²-ab)- (ab-b²)=8-(-4) - 8+4= 12.
例2 按图3-2所示的方式将点隔开分成5层,如果继续画下去,第6层画多少个点?第n层呢?


答案:
解:由每层的点数变化规律可知,第6层应画11个点,第n层应画(2n- 1)个点.
例3 某快递公司承办A,B两地的快递业务,收费标准为:货物不超过10 kg时,收费10元/kg;货物超过10 kg时,超过部分收费6元/kg.
(1)设货物为x kg,写出当x不超过10 kg和x超过10 kg时,应分别收费多少元;
(2)当货物为6.5 kg和25 kg时,应分别收多少费用?
(1)设货物为x kg,写出当x不超过10 kg和x超过10 kg时,应分别收费多少元;
(2)当货物为6.5 kg和25 kg时,应分别收多少费用?
答案:
解:
(1)当x不超过10时,应收费10x;
当x超过10时,10×10+6(x-10) = 6x+40,应收费(6x+ 40)元.
(2)当x= 6.5时,10x= 65;
当x= 25时,6x+40= 6×25+40= 190.\
因此,当货物为6.5千克和25千克时,应分别收费65元,190元
(1)当x不超过10时,应收费10x;
当x超过10时,10×10+6(x-10) = 6x+40,应收费(6x+ 40)元.
(2)当x= 6.5时,10x= 65;
当x= 25时,6x+40= 6×25+40= 190.\
因此,当货物为6.5千克和25千克时,应分别收费65元,190元
1. 填空题:
(1)单项式$-\frac{2\pi ab^{2}c}{3}$的系数是
(2)计算:$b-[a-(b-a)]= $
(3)已知$x+y= 3$,则$-2x-2y+1$的值为
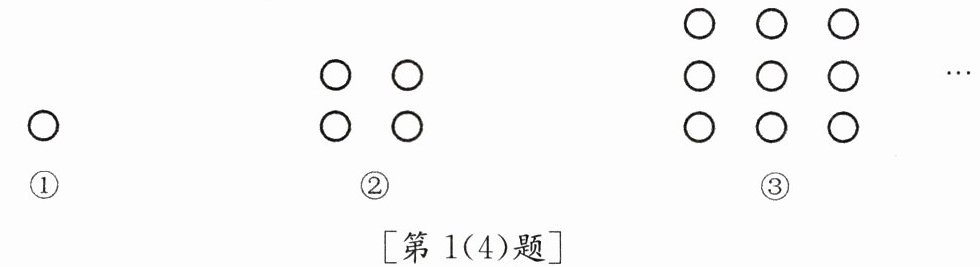
(4)如图,每个图案都由若干个小圆圈组成,照此规律,第n个图案中小圆圈的总个数用含n的代数式表示为
(5)按照规律书写代数式:$x$,$-2x^{2}$,$3x^{3}$,$-4x^{4}$,$5x^{5}$,$-6x^{6}$,…,第100项为
(1)单项式$-\frac{2\pi ab^{2}c}{3}$的系数是
$-\frac{2π}{3}$
,次数是4
,多项式$xy-2x+1$的次数是2
;(2)计算:$b-[a-(b-a)]= $
$2b-2a$
;(3)已知$x+y= 3$,则$-2x-2y+1$的值为
$-5$
;(4)如图,每个图案都由若干个小圆圈组成,照此规律,第n个图案中小圆圈的总个数用含n的代数式表示为
$n²$
;
(5)按照规律书写代数式:$x$,$-2x^{2}$,$3x^{3}$,$-4x^{4}$,$5x^{5}$,$-6x^{6}$,…,第100项为
$-2024x^{2024}$
,第101项为$2025x^{2025}$
.
答案:
$-\frac{2π}3$
4
2
2b-2a
-5
n²
-2024x^{2024}
2025x^{2025}
4
2
2b-2a
-5
n²
-2024x^{2024}
2025x^{2025}
查看更多完整答案,请扫码查看


