第102页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
3. 如图,O是线段AB的中点,C是线段OB的中点,OC= 1.5,求线段AB的长.
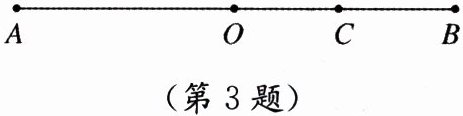
(第3题)

(第3题)
答案:
解:
∵C是线段OB的中点, OC=1.5
∴OB=2OC=3
∵O是线段AB的中点
∴AB=2OB=6
∵C是线段OB的中点, OC=1.5
∴OB=2OC=3
∵O是线段AB的中点
∴AB=2OB=6
4. 如图,已知三角形ABC.
(1)用直尺和圆规作一条线段m,使得m= BC-AC;
(2)比较m和AB的长短,并用"<"号连接.
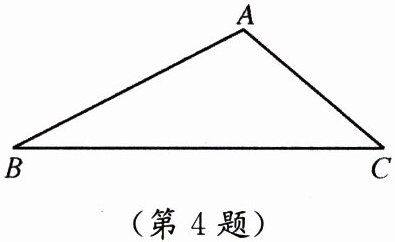
(第4题)
(1)用直尺和圆规作一条线段m,使得m= BC-AC;
(2)比较m和AB的长短,并用"<"号连接.

(第4题)
答案:
解:
(1)如图。
(2)m<AB
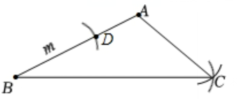
解:
(1)如图。
(2)m<AB

5. 已知点A,B,C在一条直线上,AB= 3,BC= 1.求AC的长.
答案:
解:
∵AB=3, BC=1
∴AC= AB+BC=4或AC= AB-BC=2
∴AC的长为4或2
∵AB=3, BC=1
∴AC= AB+BC=4或AC= AB-BC=2
∴AC的长为4或2
|思路方法|解答过程|知识要素|
|未知线段转化已知线段……|因为C,D分别是线段AO,BO的中点,所以CO= $\frac{1}{2}$AO,DO= $\frac{1}{2}$
(2)
|未知线段转化已知线段……|因为C,D分别是线段AO,BO的中点,所以CO= $\frac{1}{2}$AO,DO= $\frac{1}{2}$
BO
.因为AB= 10,所以CD= CO+DO= $\frac{1}{2}$AO+$\frac{1}{2}$BO
= $\frac{1}{2}$AB
= 5
.|线段中点的定义线段的和、差等式的性质……|(2)
解:不会;如果点O运动到点B的右侧,此时有$CD=CO-DO=\frac{1}{2}(AO-BO)=\ \frac{1}2AB=5$当点O运动到点A的左侧,同样有$CD=\ \frac{1}2AB=5$故CD的长不会发生变化
答案:
BO
BO
AB
5
解:不会;如果点O运动到点B的右侧,
此时有$CD=CO-DO=\frac{1}{2}(AO-BO)=\ \frac{1}2AB=5$
当点O运动到点A的左侧,同样有$CD=\ \frac{1}2AB=5\ $
故CD的长不会发生变化
BO
AB
5
解:不会;如果点O运动到点B的右侧,
此时有$CD=CO-DO=\frac{1}{2}(AO-BO)=\ \frac{1}2AB=5$
当点O运动到点A的左侧,同样有$CD=\ \frac{1}2AB=5\ $
故CD的长不会发生变化
查看更多完整答案,请扫码查看


