《2025年学习与评价江苏凤凰教育出版社七年级数学上册苏科版》

3. 求下列各式的值:
(1)$3a+2b-5a-b$,其中$a= -2,b= 1;$ (2)$3x-4x^{2}+7-3x+2x^{2}+1$,其中$x= -3.$

答案： 解:
(1)原式=(3a-5a)+(2b-b)
          \ \ \ \ \ \ \ \ \ \ =-2a+b
将a=-2, b=1代入,得
原式=(-2)×(-2)+1=5
解:
(2)原式=(3x-3x)+(-4x²+2x²)+7+1
\ \ \ \ \ \ \ =-2x²+8
将x=-3代入,得
原式=(-2)×(-3)²+8=-10

4. (1)x的4倍与x的5倍的和是多少?
(2)x的3倍与x的一半的差是多少?

答案： 解：
(1)4x+5x=9x
$(2) 3x-\frac{1}2x=\frac{5}2x$

5. 如图,长方形由边长为a的1个大正方形和边长为b的3个小正方形组成.

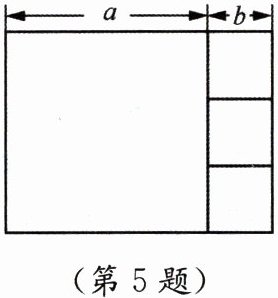
(1)a与b的数量关系是怎样的?
(2)这个长方形的周长是多少(结果只用含b的代数式表示)?

答案： 解:
(1)从右图可以看出,大正方形的边长是小正方形边长的3倍，
即a=3b
(2) 2×(a+b+a)=4a+2b
将a=3b代入，得
4a+2b=4×3b+2b=14b
∴这个长方形的周长为14b

6. 阅读材料:利用合并同类项可以将多项式化简,如$5a-3a+a= (5-3+1)a= 3a$.类似地,我们把$(x+y)$看成一个整体,则$5(x+y)-3(x+y)+(x+y)= (5-3+1)(x+y)= 3(x+y)$."整体思想"是数学解题中的一种重要的思想,它在多项式的化简与求值中应用广泛.
尝试应用：
(1)把$(x-y)^{2}$看成一个整体,$3(x-y)^{2}-6(x-y)^{2}+2(x-y)^{2}$合并的结果是$-(x-y)^{2}$;
(2)已知$a^{2}-2b= 1$,求$3-2a^{2}+4b$的值.
解:(2)原式=-2(a²-2b)+3
=-2×1+3
=-2+3
=1

答案： -(x-y)²
解:
(2)原式=-2(a²-2b)+3
=-2×1+3
=-2+3
=1