《2025年学习与评价江苏凤凰教育出版社七年级数学上册苏科版》

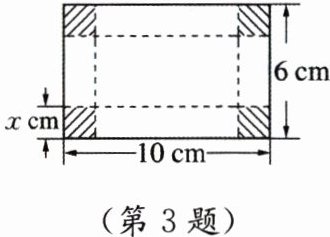
3. 如图,长方形纸板的长为10 cm,宽为6 cm,四角割去边长为x cm的小正方形后折叠形成一个无盖长方体.该长方体的体积是多少?(用含x的代数式表示)

答案： 解:
∵长方体的长为$(10-2x)\ \mathrm {cm}，$宽为$(6-2x)\ \mathrm {cm}，$高为$x\ \mathrm {cm}$
∴长方体的体积为$(10-2x)(6-2x)x\ \mathrm {cm}³$

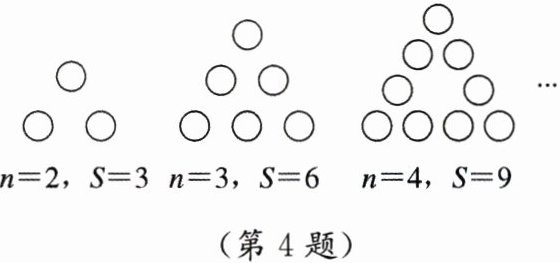
4. 如图是由若干圆圈组成的形如三角形的图案,每条边(包括两个端点)有$ n(n＞1) $个圆圈,每个图案圆圈的总数是S,按此规律,推断S与n之间的表达式.
分析甲、乙、丙三名学生的思考过程和结果是否正确.
甲：考虑到三角形3条边上的圆圈个数都是n个,所以共有圆圈总数为$ S = 3n $(个).
乙：考虑到三角形3条边上的圆圈个数,第1条边有n个,第2条、第3条边都有$ n - 1 $个,所以共有圆圈总数为$ S = n + n - 1 + n - 1 = 3n - 2 $(个).
丙：当$ n = 2 $时,$ S = 3×(2 - 1) $;当$ n = 3 $时,$ S = 3×(3 - 1) $;当$ n = 4 $时,$ S = 3×(4 - 1) $.由此推断第n个图案圆圈总数为$ S = 3(n - 1) $(个).

答案： 解:甲、乙的过程和结果都不正确，
因为甲和乙都有重复计算的部分,
丙的过程和结果都正确。

5. 观察下列式子:
① $ 1 = 1^2 $,
② $ 1 + 3 = 2^2 $,
③ $ 1 + 3 + 5 = 3^2 $,
…
探索以上式子的规律,解决下列问题:
(1) $ 1 + 3 + 5 + … + 17 = $9$^2 $;
(2) 写出第n个等式;
(3) 利用(2)中的等式,计算$ 19 + 21 + 23 + … + 99 $.
解: (2) 1+3+5+...+2n-1=n²
(3)原式=(1+3+5+...+99)-(1+3+5+...+17)
\ \ \ \ \ \ \ =50²-9²
\ \ \ \ \ \ \ =2500-81
\ \ \ \ \ \ \ =2419

答案： 9
解:
(2) 1+3+5+...+2n-1=n²
(3)原式=(1+3+5+...+99)-(1+3+5+...+17)
\ \ \ \ \ \ \ =50²-9²
\ \ \ \ \ \ \ =2500-81
\ \ \ \ \ \ \ =2419

6. 数学活动课上,老师拿出如图所示的两个单位长度不同的数轴A和数轴B模型,当两个数轴的原点对齐时,数轴A上表示2的点与数轴B上表示3的点恰好对齐.数轴A上表示数x的点与数轴B上表示哪个数的点对齐?

答案： 答：数轴A上表示2的点与
数轴B上表示3的点恰好对齐.
数轴A上表示数x的点与数轴
B上表示1.5x的点对齐。