《2025年课堂点睛八年级数学上册北师大版宁夏专版》

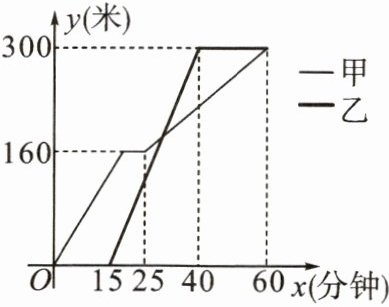
18. (数形结合法)甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行 15 分钟到缆车站,再乘坐缆车直达山顶.甲、乙距山脚的垂直高度 y(米)与甲登山的时间 x(分钟)之间的函数图象如图所示.
(1)当 $ 15 ≤ x ≤ 40 $ 时,求乙距山脚的垂直高度 y 与 x 之间的函数关系式；
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.

答案：
(1)解:设乙距山脚的垂直高度$y$与$x$之间的函数关系式为$y = kx + b$,$\because$直线过$(15,0)$和$(40,300)$,$\therefore \begin{cases}15k + b = 0\\40k + b = 300\end{cases}$,解得$\begin{cases}k = 12\\b = -180\end{cases}$,$\therefore$当$15\leqslant x\leqslant 40$时,乙距山脚的垂直高度$y$与$x$之间的函数关系式为$y = 12x - 180$.
(2)当$25\leqslant x\leqslant 60$时,设甲的函数表达式为$y = mx + n$,将$(25,160)$和$(60,300)$代入得$\begin{cases}160 = 25m + n\\300 = 60m + n\end{cases}$,解得$\begin{cases}m = 4\\n = 60\end{cases}$,$\therefore y = 4x + 60(25\leqslant x\leqslant 60)$.$\because$乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度也相同,$\therefore \begin{cases}y = 12x - 180\\y = 4x + 60\end{cases}$,解得$\begin{cases}x = 30\\y = 180\end{cases}$,$\therefore$乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度为180米.

19. 已知方程 $ ( m - 2 ) x ^ { | m | - 1 } + y ^ { 2 n - 1 } = 4 $ 是关于 x,y 的二元一次方程,则 $ m + n = $-1.

答案： -1

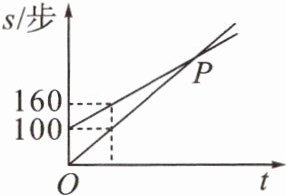
20. (贵州省中考改编)我国古代数学经典著作《九章算术》记载：“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之?”如图是善行者与不善行者行走路程 s(单位:步)关于善行者的行走时间 t 的函数图象,则两图象交点 P 的纵坐标是250.

答案： 250

21. 已知一次函数 $ y _ { 1 } = k x + b $ 与 $ y = - 2 x $ 的图象平行,且与 x 轴的交点 A 的横坐标为 2.
(1)填空: $ k = $____,$ b = $____；
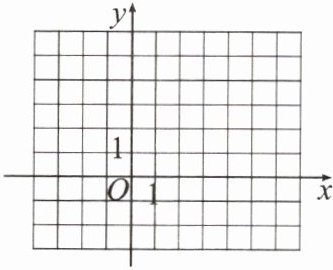
(2)在下面的平面直角坐标系中,画出一次函数 $ y _ { 1 } $ 和 $ y _ { 2 } = x + 1 $ 的图象,并借助图象求方程组 $ \left\{ \begin{array} { l } { y = k x + b, } \\ { y = x + 1 } \end{array} \right. $ 的解；
(3)若 $ y _ { 2 } $ 与 x 轴的交点为 B,$ y _ { 1 } $ 和 $ y _ { 2 } $ 两图象的交点为 C,在 $ y _ { 2 } $ 的图象上是否存在点 P,使得 $ △OBP $ 的面积与 $ △ABC $ 的面积相等? 若存在,请求出符合条件的点 P 的坐标;若不存在,请说明理由.

答案：

(1)-2　4　
(2)解:画出一次函数$y_1$和$y_2 = x + 1$的图象如图所示.由图象可知一次函数$y_1$和$y_2 = x + 1$的图象的交点坐标为$(1,2)$,$\therefore$方程组$\begin{cases}y = kx + b\\y = x + 1\end{cases}$的解为$\begin{cases}x = 1\\y = 2\end{cases}$.
(3)令$y = 0$,则$x + 1 = 0$,解得$x = -1$,$\therefore B(-1,0)$.$\therefore OB = 1$.$\because A(2,0)$,$C(1,2)$,$\therefore S_{\triangle ABC}=\frac{1}{2}× (2 + 1)× 2 = 3$.设$P(x,x + 1)$,$\because \triangle OBP$的面积与$\triangle ABC$的面积相等,$\therefore \frac{1}{2}× 1× |x + 1| = 3$,解得$x = 5$或$x = -7$.$\therefore$点$P$的坐标为$(5,6)$或$(-7,-6)$.