第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 已知直线$y = x + b和y = ax - 3交于点P(2,1)$,则关于$x的方程x + b = ax - 3$的解为
x=2
。
答案:
x=2
8. (陕西省中考)在同一平面直角坐标系中,直线$y = -x + 4与y = 2x + m相交于点P(3,n)$,则关于$x$,$y的方程组\begin{cases}x + y - 4 = 0\\2x - y + m = 0\end{cases} $的解为
$\left\{\begin{array}{l}x=3,\\ y=1\end{array}\right.$
。
答案:
$\left\{\begin{array}{l}x=3,\\ y=1\end{array}\right.$
9. (教材第129页随堂练习第3题变式)若方程组$\begin{cases}y = kx + 3\\y = (3k + 1)x + 2\end{cases} $无解,则$y = kx - 2$的图象不经过第
一
象限。
答案:
一
10. 如图,在平面直角坐标系中,已知正比例函数$y = \frac{3}{4}x与一次函数y = -x + 7的图象交于点A$。
(1)求点$A$的坐标;
(2)设$x轴上有一点P(a,0)$,过点$P作x$轴的垂线(垂线位于点$A$的右侧),分别交$y = \frac{3}{4}x和y = -x + 7的图象于点B$,$C$,连接$OC$,若$BC = 7$,求$\triangle OBC$的面积。
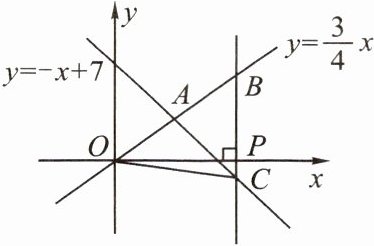
(1)求点$A$的坐标;
(2)设$x轴上有一点P(a,0)$,过点$P作x$轴的垂线(垂线位于点$A$的右侧),分别交$y = \frac{3}{4}x和y = -x + 7的图象于点B$,$C$,连接$OC$,若$BC = 7$,求$\triangle OBC$的面积。

答案:
(1)解:由题意得$\left\{\begin{array}{l}y=\dfrac{3}{4}x,\\ y=-x+7,\end{array}\right.$解得$\left\{\begin{array}{l}x=4,\\ y=3,\end{array}\right.$所以点A的坐标为(4,3).
(2)因为P(a,0),所以B(a,$\dfrac{3}{4}a$),C(a,-a+7),所以BC=$\dfrac{3}{4}a$-(-a+7)=$\dfrac{7}{4}a$-7,所以$\dfrac{7}{4}a$-7=7,解得a=8,所以$S_{\triangle OBC}=\dfrac{1}{2}BC\cdot OP=\dfrac{1}{2}× 7× 8=28$.
(1)解:由题意得$\left\{\begin{array}{l}y=\dfrac{3}{4}x,\\ y=-x+7,\end{array}\right.$解得$\left\{\begin{array}{l}x=4,\\ y=3,\end{array}\right.$所以点A的坐标为(4,3).
(2)因为P(a,0),所以B(a,$\dfrac{3}{4}a$),C(a,-a+7),所以BC=$\dfrac{3}{4}a$-(-a+7)=$\dfrac{7}{4}a$-7,所以$\dfrac{7}{4}a$-7=7,解得a=8,所以$S_{\triangle OBC}=\dfrac{1}{2}BC\cdot OP=\dfrac{1}{2}× 7× 8=28$.
11. (核心素养·应用意识)已知二元一次方程$x + y = 5$,通过列举将方程的解写成下列表格的形式:
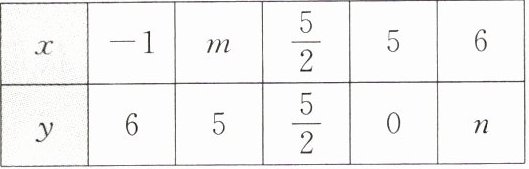
如果将二元一次方程的解所包含的未知数$x$的值对应平面直角坐标系中一个点的横坐标,未知数$y$的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应平面直角坐标系中的一个点,例如:方程$x + y = 5的解\begin{cases}x = 2\\y = 3\end{cases} 的对应点是(2,3)$。
(1)表格中的$m = $______,$n = $______;
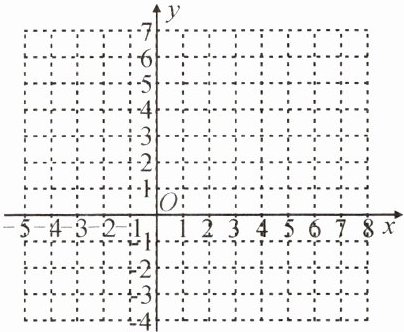
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,请在所给的平面直角坐标系中画出这五个点;根据这些点猜想方程$x + y = 5$的解的对应点所组成的图形是______,并写出它的两个特征:①______,②______;
(3)若点$P(-2a,a - 1)恰好落在x + y = 5$的解对应的点组成的图形上,求$a$的值。
(1)表格中的$m = $
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,请在所给的平面直角坐标系中画出这五个点;根据这些点猜想方程$x + y = 5$的解的对应点所组成的图形是
(3)若点$P(-2a,a - 1)恰好落在x + y = 5$的解对应的点组成的图形上,求$a$的值。

如果将二元一次方程的解所包含的未知数$x$的值对应平面直角坐标系中一个点的横坐标,未知数$y$的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应平面直角坐标系中的一个点,例如:方程$x + y = 5的解\begin{cases}x = 2\\y = 3\end{cases} 的对应点是(2,3)$。

(1)表格中的$m = $______,$n = $______;
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,请在所给的平面直角坐标系中画出这五个点;根据这些点猜想方程$x + y = 5$的解的对应点所组成的图形是______,并写出它的两个特征:①______,②______;
(3)若点$P(-2a,a - 1)恰好落在x + y = 5$的解对应的点组成的图形上,求$a$的值。
(1)表格中的$m = $
0
,$n = $-1
;(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,请在所给的平面直角坐标系中画出这五个点;根据这些点猜想方程$x + y = 5$的解的对应点所组成的图形是
直线
,并写出它的两个特征:①图象经过第一、二、四象限
,②图象从左向右呈下降趋势
;(3)若点$P(-2a,a - 1)恰好落在x + y = 5$的解对应的点组成的图形上,求$a$的值。
解:由题意,得-2a+a-1=5.解得a=-6.
答案:
(1)0 -1
(2)图略. 直线 图象经过第一、二、四象限 图象从左向右呈下降趋势
(3)解:由题意,得-2a+a-1=5.解得a=-6.
(1)0 -1
(2)图略. 直线 图象经过第一、二、四象限 图象从左向右呈下降趋势
(3)解:由题意,得-2a+a-1=5.解得a=-6.
查看更多完整答案,请扫码查看


