第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
5. (扬州市中考)如图,已知一次函数 $ y = kx + b $($ k \neq 0 $)的图象分别与 $ x $、$ y $ 轴交于 $ A $、$ B $ 两点,若 $ OA = 2 $,$ OB = 1 $,则关于 $ x $ 的方程 $ kx + b = 0 $ 的解为
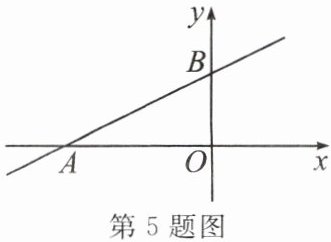
$x = -2$
。
答案:
$x = -2$
6. 若等腰三角形的周长为100cm,则能反映腰长 $ y $ 与底边 $ x $ 之间关系的图象是(
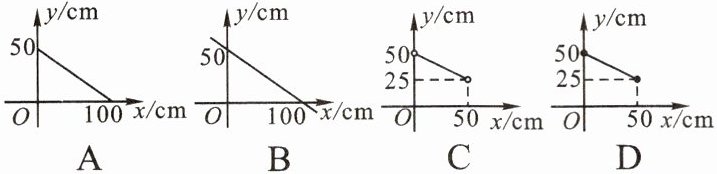
C
)
答案:
C
7. 如图,已知直线 $ y = ax - b $,则关于 $ x $ 的方程 $ ax - 1 = b $ 的解是 $ x = $(
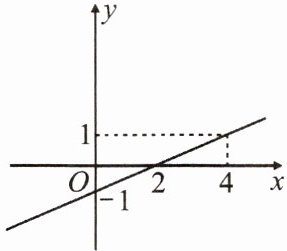
A.4
B.1
C.2
D.-1
A
)
A.4
B.1
C.2
D.-1
答案:
A
8. 如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度 $ y $(cm)和注水时间 $ x $(s)之间的关系满足如图2中的图象,则至少需要
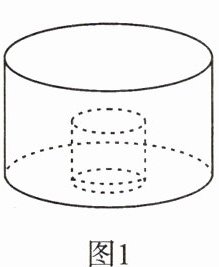
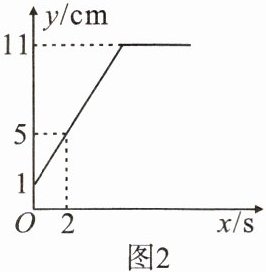
5
s才能把小水杯注满。

答案:
5
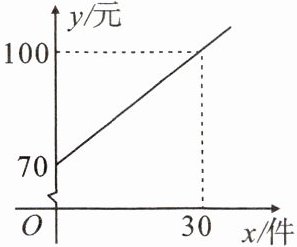
9. (教材第98页随堂练习第1题变式)某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示。
(1)求每位“快递小哥”的日收入 $ y $(元)与日派送量 $ x $(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
(1)求每位“快递小哥”的日收入 $ y $(元)与日派送量 $ x $(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?

答案:
(1)解:设每位“快递小哥”的日收入 $y$(元)与日派送量 $x$(件)之间的函数关系式为 $y = kx + b$,将 $(0,70)$,(30,100)代入 $y = kx + b$,得 $b = 70$,$30k + b = 100$,解得 $k = 1$,
∴每位“快递小哥”的日收入 $y$(元)与日派送量 $x$(件)之间的函数关系式为 $y = x + 70$.
(2)当 $y = 110$ 时,$x + 70 = 110$,解得 $x = 40$.
∴“快递小哥”的日收入不少于 110 元,则他至少要派送 40 件.
(1)解:设每位“快递小哥”的日收入 $y$(元)与日派送量 $x$(件)之间的函数关系式为 $y = kx + b$,将 $(0,70)$,(30,100)代入 $y = kx + b$,得 $b = 70$,$30k + b = 100$,解得 $k = 1$,
∴每位“快递小哥”的日收入 $y$(元)与日派送量 $x$(件)之间的函数关系式为 $y = x + 70$.
(2)当 $y = 110$ 时,$x + 70 = 110$,解得 $x = 40$.
∴“快递小哥”的日收入不少于 110 元,则他至少要派送 40 件.
10. (核心素养·应用意识)张师傅在铺地板时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图①,然后,他用这8块瓷砖又拼出一个大正方形,如图②,中间恰好空出一个边长为1的小正方形(阴影部分),假设小长方形瓷砖的长为 $ y $,宽为 $ x $。
(1)求出图①中 $ y $ 与 $ x $ 之间的函数表达式(不需要写出自变量 $ x $ 的取值范围);
(2)求出图②中 $ y $ 与 $ x $ 之间的函数表达式(不需要写出自变量 $ x $ 的取值范围);
(3)在图③中作出(1)(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义。

(1)求出图①中 $ y $ 与 $ x $ 之间的函数表达式(不需要写出自变量 $ x $ 的取值范围);
(2)求出图②中 $ y $ 与 $ x $ 之间的函数表达式(不需要写出自变量 $ x $ 的取值范围);
(3)在图③中作出(1)(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义。

答案:
(1)解:由题图①,得 $3y = 5x$,得 $y = \frac{5}{3}x$.
(2)由题图②,得 $2x - y = 1$,即 $y = 2x - 1$.
(3)画出函数图象略.交点坐标为 $(3,5)$.实际意义:小长方形瓷砖的长为 5,宽为 3 时,既能围成题图①所示的图形,又能围成题图②所示的图形.
(1)解:由题图①,得 $3y = 5x$,得 $y = \frac{5}{3}x$.
(2)由题图②,得 $2x - y = 1$,即 $y = 2x - 1$.
(3)画出函数图象略.交点坐标为 $(3,5)$.实际意义:小长方形瓷砖的长为 5,宽为 3 时,既能围成题图①所示的图形,又能围成题图②所示的图形.
查看更多完整答案,请扫码查看


