第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 在 $\triangle ABC$ 中,$AB = 15$,$AC = 20$,$D$ 是 $BC$ 边所在直线上的点,$AD = 12$,$BD = 9$,则 $BC = $
25 或 7
。
答案:
25 或 7
8. 一个三角形的三边之比为 $5:12:13$,周长为 $60$,则它的面积是 (
A.$120$
B.$144$
C.$196$
D.$60$
A
)A.$120$
B.$144$
C.$196$
D.$60$
答案:
A
9. 在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中,则当 $a = 24$ 时,$b + c$ 的值为 (
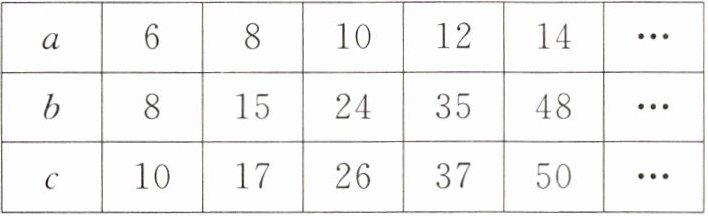
A.$250$
B.$288$
C.$300$
D.$574$
B
)
A.$250$
B.$288$
C.$300$
D.$574$
答案:
B
10. 如图,每个小正方形的边长为 $1$,则 $\angle ABC$ 的度数为
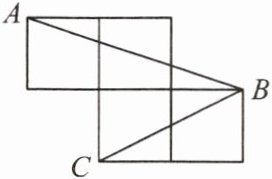
$45^{\circ }$
。
答案:
$45^{\circ }$
11. 若 $|x - 5|+|y - 12|+(z - 13)^{2}= 0$,则以 $x$,$y$,$z$ 为三边的三角形的面积为
30
。
答案:
30
12. (教材第 $11$ 页随堂练习第 $2$ 题变式)如图所示,在正方形 $ABCD$ 中,$E$ 为 $AB$ 的中点,$F$ 是 $AD$ 上一点,且 $AF= \frac{1}{4}AD$,试判断 $\triangle FEC$ 的形状,并说明理由。
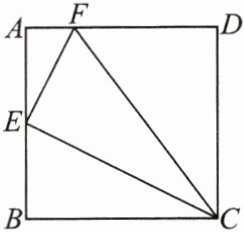

答案:
解:$\triangle FEC$为直角三角形,理由:设正方形边长为$4a$,则$AE=BE=2a,AF=a,FD=3a$.在$Rt\triangle AEF$中,$EF^{2}=a^{2}+(2a)^{2}=5a^{2}$,在$Rt\triangle BCE$中,$CE^{2}=(2a)^{2}+(4a)^{2}=20a^{2}$,在$Rt\triangle CDF$中,$CF^{2}=(3a)^{2}+(4a)^{2}=25a^{2}$,所以$CF^{2}=CE^{2}+EF^{2}$,所以$\triangle FEC$是直角三角形.
如图,在四边形 $ABCD$ 中,$AB = 3cm$,$AD = 4cm$,$BC = 13cm$,$CD = 12cm$,且 $\angle A = 90^{\circ}$,则四边形 $ABCD$ 的面积为 (
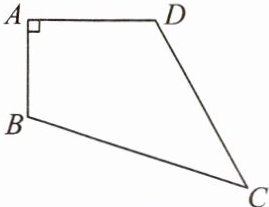
A.$12cm^{2}$
B.$18cm^{2}$
C.$22cm^{2}$
D.$36cm^{2}$
D
)
A.$12cm^{2}$
B.$18cm^{2}$
C.$22cm^{2}$
D.$36cm^{2}$
答案:
D
【变式】如图,已知 $\angle ADC = 90^{\circ}$,$AD = 8m$,$CD = 6m$,$BC = 24m$,$AB = 26m$,则图中阴影部分的面积为
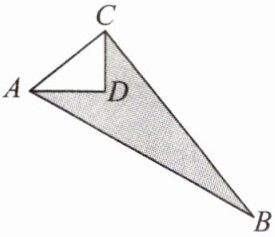
$96\mathrm{m}^{2}$
。
答案:
$96\mathrm{m}^{2}$
【拓展】某小区将对广场一块三角形空地进行绿化,如图,等腰三角形 $ABC$ 的底边 $BC$ 长为 $10m$,点 $D$ 是 $AC$ 上的一点,$BD = 8m$,$CD = 6m$。
(1)求证:$BD\perp AC$;
(2)三角形空地的面积为______$m^{2}$。
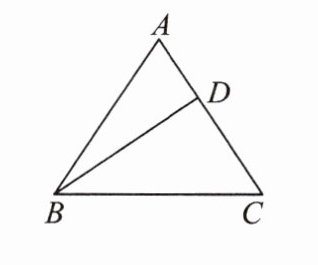
(1)求证:$BD\perp AC$;
(2)三角形空地的面积为______$m^{2}$。

(1)证明:在$\triangle BDC$中,$BC=10\mathrm{m},BD=8\mathrm{m},CD=6\mathrm{m},\therefore BD^{2}+CD^{2}=8^{2}+6^{2}=10^{2}=BC^{2},\therefore \angle BDC=90^{\circ },\therefore BD\perp AC$.
(2)$\frac{100}{3}$
(2)$\frac{100}{3}$
答案:
(1)证明:在$\triangle BDC$中,$BC=10\mathrm{m},BD=8\mathrm{m},CD=6\mathrm{m},\therefore BD^{2}+CD^{2}=8^{2}+6^{2}=10^{2}=BC^{2},\therefore \angle BDC=90^{\circ },\therefore BD\perp AC$.
(2)$\frac{100}{3}$
(1)证明:在$\triangle BDC$中,$BC=10\mathrm{m},BD=8\mathrm{m},CD=6\mathrm{m},\therefore BD^{2}+CD^{2}=8^{2}+6^{2}=10^{2}=BC^{2},\therefore \angle BDC=90^{\circ },\therefore BD\perp AC$.
(2)$\frac{100}{3}$
查看更多完整答案,请扫码查看


