《2025年同步练习册山东五年级数学上册青岛版》

(1)三角形的面积= (底×高÷2)。如果用a表示三角形的底,h表示三角形的高,S表示三角形的面积,那么S= (ah÷2)。

答案： 解析：题目考查三角形的面积公式。
答案：底×高÷2；$ah÷2$。

(2)一个三角形的底是5厘米,高是7厘米,面积是(17.5)平方厘米。

答案： 解析：本题考查三角形面积的计算。三角形面积的计算公式为底乘以高再除以2。给定的三角形底是5厘米，高是7厘米，所以面积计算如下：
$面积 = \frac{底 × 高}{2}$
$面积 = \frac{5 × 7}{2}$
$面积 = \frac{35}{2}$
$面积 = 17.5 (平方厘米)$
答案：17.5

(3)一个三角形的面积是14平方分米,底是7分米,高是(4)分米。

答案： 解析：本题可根据三角形的面积公式来求解三角形的高。
三角形的面积公式为$S = \frac{1}{2}ah$（其中$S$表示三角形的面积，$a$表示三角形的底，$h$表示三角形的高）。
已知三角形面积$S = 14$平方分米，底$a = 7$分米，将其代入面积公式，通过变形可求出高$h$。
由$S=\frac{1}{2}ah$可得$h = 2S÷ a$。
答案：
把$S = 14$平方分米，$a = 7$分米代入$h = 2S÷ a$可得：
$h=2×14÷7$
$=28÷7$
$ = 4$（分米）
所以高是$4$分米。

(4)一个三角形的面积是4.8平方米,与它等底等高的平行四边形的面积是(9.6)平方米。

答案： 解析：题目考查三角形和平行四边形面积的关系。对于等底等高的三角形和平行四边形，平行四边形的面积是三角形面积的两倍。因为三角形的面积公式是$\frac{1}{2} × \text{底} × \text{高}$，而平行四边形的面积公式是$\text{底} × \text{高}$。
答案：9.6平方米。

(5)一个等腰直角三角形的一条直角边是10厘米,它的面积是(50)平方厘米。

答案： 解析：题目考查等腰直角三角形的面积计算。等腰直角三角形的两条直角边相等，且其中一条直角边可作为三角形的底，另一条直角边作为高。根据三角形面积公式$S = \frac{1}{2}ah$（这里$a$为底，$h$为高），已知一条直角边是$10$厘米，即底$a = 10$厘米，高$h = 10$厘米，代入公式计算面积。
答案：
$S=\frac{1}{2}×10×10 = 50$（平方厘米）
故答案为：$50$。

(6)下图平行四边形的面积是25平方厘米,阴影部分的面积是(12.5)平方厘米。

答案： 解析：本题考查三角形和平行四边形面积之间的关系。
已知平行四边形的面积公式为$S = a× h$（其中$S$表示面积，$a$表示底边长，$h$表示这条底边对应的高）。
观察图形可知，阴影部分为三角形，该三角形与平行四边形等底等高。
三角形的面积公式为$S_{\triangle}=\frac{1}{2}× a× h$（其中$S_{\triangle}$表示三角形面积，$a$表示底边长，$h$表示这条底边对应的高）。
由于三角形与平行四边形等底等高，所以三角形的面积是平行四边形面积的一半。
计算：
已知平行四边形的面积是25平方厘米，根据上述关系可得阴影部分三角形的面积为：$25÷2 = 12.5$（平方厘米）。
答案：12.5。

2.火眼金睛辨对错。
(1)三角形的面积是平行四边形面积的一半。(×)
(2)如果两个三角形的面积相等,那么它们的底和高也分别相等。(×)
(3)两个面积相等的三角形一定能拼成一个平行四边形。(×)

答案： 解析：
(1) 题目考查三角形和平行四边形的面积关系。只有当三角形与平行四边形等底等高时，三角形的面积才是平行四边形面积的一半。题目没有给出这样的条件，所以此说法是错误的。
(2) 题目考查三角形面积公式的应用。三角形的面积公式是$S = \frac{1}{2} × \text{底} × \text{高}$。面积相等不代表底和高分别相等，只要底和高的乘积相等即可。例如，底为4、高为3的三角形和底为6、高为2的三角形面积都是6，但底和高并不相等。所以此说法是错误的。
(3) 题目考查三角形的拼接。两个面积相等的三角形不一定能拼成一个平行四边形。它们需要是完全相同的两个三角形（即形状和大小都一样）才能拼成一个平行四边形。仅仅面积相等并不足以保证它们能拼接。所以此说法是错误的。
答案：
(1) ×
(2) ×
(3) ×

3.计算下列三角形的面积。

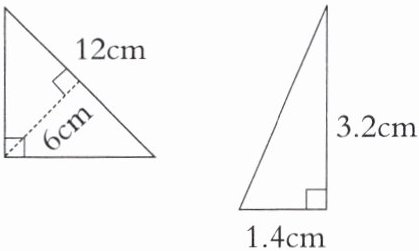
答案： 解析：本题考查三角形面积公式的应用，三角形面积公式为$S = \frac{1}{2}ah$（其中$S$表示面积，$a$表示底边长，$h$表示这条底边对应的高）。
答案：
第一个三角形：
$S=\frac{1}{2}× 12× 6 = 36$（$cm^2$）
第二个三角形：
$S=\frac{1}{2}× 1.4× 3.2 = 2.24$（$cm^2$）
综上，第一个三角形面积为$36cm^2$，第二个三角形面积为$2.24cm^2$。

(1)任意两个完全一样的三角形都可以拼成一个(C)。
A.长方形
B.正方形
C.平行四边形

答案： 解析：
这个问题考查的是三角形的拼接以及平行四边形的形成。
两个完全一样的三角形意味着它们的形状和大小都完全相同。
当我们将两个这样的三角形以它们的一组对应的边相拼接时，它们会形成一个四边形。
特别地，由于这两个三角形是完全一样的，所以拼接形成的四边形的对边会是平行且相等的，这就形成了一个平行四边形。
长方形和正方形都是特殊的平行四边形，但它们需要满足额外的条件（如长方形的对边平行且相等，且四个角都是直角；正方形的四条边都相等且四个角都是直角）。
题目中并没有给出这样的条件，所以我们不能确定拼接形成的一定是长方形或正方形。
因此我们可以确定拼接形成的是一个平行四边形。
答案：
C 平行四边形。

(2)下列说法正确的是(A)。
A.等底等高的三角形,面积一定相等
B.两个三角形等底等高,形状一定完全相同
C.直角三角形只有一条高

答案： 解析：
A选项：根据三角形面积的计算公式，面积 $S = \frac{1}{2} × \text{底} × \text{高}$，如果两个三角形的底和高都相等，那么它们的面积一定相等。所以A选项是正确的。
B选项：两个三角形等底等高，并不意味着它们的形状一定完全相同。例如，可以构造一个直角三角形和一个等腰三角形，使它们有相同的底和高，但它们的形状显然不同。所以B选项是错误的。
C选项：直角三角形实际上有三条高。除了我们通常看到的垂直于底边的高之外，还有两条高分别是两条直角边。所以C选项是错误的。
答案：A。

(3)等底等面积的三角形与平行四边形的高相比较,(A)。
A.三角形的高是平行四边形的两倍
B.三角形的高和平行四边形的高相等
C.三角形的高是平行四边形的一半
D.无法确定

答案： 解析：
首先，我们要明确三角形和平行四边形的面积计算公式，并理解题目中的“等底等面积”条件。
三角形的面积公式为：$S_{\text{三角形}} = \frac{1}{2} × \text{底} × \text{高}$
平行四边形的面积公式为：$S_{\text{平行四边形}} = \text{底} × \text{高}$
由题意知，三角形和平行四边形的底相等，且面积也相等。我们可以设三角形的底为b，高为$h_1$，平行四边形的高为$h_2$。
根据面积公式，我们有：
$\frac{1}{2} × b × h_1 = b × h_2$
由于b不为0（因为底是存在的），我们可以两边同时除以b，得到：
$\frac{1}{2} × h_1 = h_2$
进一步整理，得到：
$h_1 = 2h_2$
这说明三角形的高是平行四边形高的两倍。
答案：
A.三角形的高是平行四边形的两倍。

5.如图所示,流动红旗的底是28厘米,高是35厘米。学校要做12面这样的流动红旗奖励先进班级,至少需要多少平方米的丝绸?

答案： 28×35÷2=490(平方厘米)
490×12=5880(平方厘米)
5880平方厘米=0.588平方米
答:至少需要0.588平方米的丝绸。