《2025年同步练习册山东五年级数学上册青岛版》

(1)已知32×8= 256,那么3.2×8= (25.6),32×0.8= (25.6),32×0.08= (2.56)。

答案： 解析：题目考查小数乘整数的知识点。当一个因数不变，另一个因数扩大或缩小$10$倍、$100$倍、$1000$倍……时，积也随着扩大或缩小相同的倍数。
答案：
$3.2×8 = 25.6$；
$32×0.8 = 25.6$；
$32×0.08 = 2.56$。

(2)15个0.18的和是(2.7)。

答案： 解析：本题考查小数乘整数的意义，即求几个相同加数的和的简便运算。用乘法计算，列式为$0.18×15$。
答案：$0.18×15 = 2.7$。

(3)0.5的32倍是(16)。

答案： 解析：本题可根据小数乘整数的意义来求解，即求一个数的几倍是多少用乘法计算。
答案：$0.5×32 = 16$，所以0.5的32倍是$16$。

(4)两个因数的积是23.6。一个因数不变,另一个因数扩大到原来的100倍,积是(2360)。

答案： 解析：题目考察的是因数变化对积的影响。当一个因数不变，另一个因数扩大到原来的100倍时，积也会扩大到原来的100倍。
答案：2360。

2.直接写得数。
0.5×2=1
0.6×50=30
3.5×2=7
5.5×4=22
60×1.2=72
3.4×200=680
30×0.04=1.2
25×0.4=10

答案： 0.5×2=1
0.6×50=30
3.5×2=7
5.5×4=22
60×1.2=72
3.4×200=680
30×0.04=1.2
25×0.4=10

3.用竖式计算。
36×0.25=9
```
36
×0.25
----
180
72
----
9.00
```
1.15×32=36.8
```
1.15
× 32
-----
230
345
-----
36.80
```
0.15×320=48
```
0.15
×320
-----
30
30
0
-----
48.00
```
78×1.05=81.9
```
78
×1.05
-----
390
0
78
-----
81.90
```

答案：

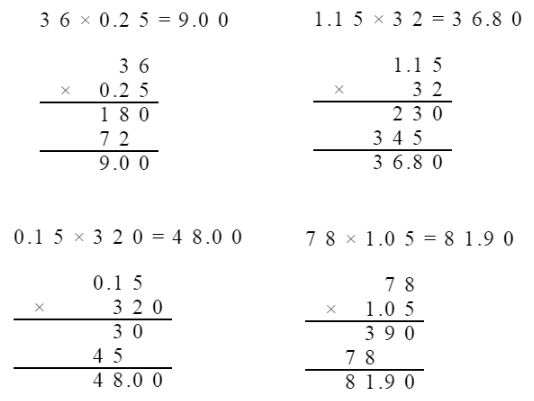
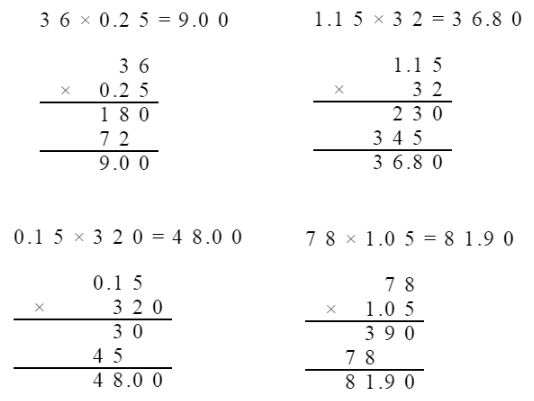
(1)下列各式中,结果是32.4的是(B)。
A.85×0.92
B.72×0.45
C.88×0.48

答案： 解析：本题可根据小数乘法的计算方法，分别计算出选项中算式的结果，再与$32.4$进行比较。
选项A：计算$85×0.92$，先按照整数乘法算出$85×92 = 7820$，因数中一共有两位小数，则从积的右边起数出两位点上小数点，可得$85×0.92 = 78.2$，该选项不符合要求。
选项B：计算$72×0.45$，先算$72×45 = 3240$，因数中一共有两位小数，从积的右边起数出两位点上小数点，即$72×0.45 = 32.4$，该选项符合要求。
选项C：计算$88×0.48$，先算$88×48 = 4224$，因数中一共有两位小数，从积的右边起数出两位点上小数点，可得$88×0.48 = 42.24$，该选项不符合要求。
答案：B

(2)妈妈带100元钱去超市买了4千克苹果,每千克苹果卖7.5元,收银员阿姨应找给妈妈(B)。
A.60元
B.70元
C.80元

答案： 7.5×4=30(元)
100-30=70(元)
B

5.光明超市新进一批牛奶,其中纯牛奶有210箱,酸奶的数量是纯牛奶的1.6倍。新进多少箱酸奶？

答案： 解析：题目考查小数乘整数的计算。
首先，我们知道纯牛奶有210箱。
接着，题目说酸奶的数量是纯牛奶的1.6倍。
那么，我们可以用纯牛奶的数量乘以1.6来得到酸奶的数量。
计算过程为：
$210 × 1.6 = 336$（箱）。
答案：新进336箱酸奶。

6.亮亮家到学校大约有1.3千米,他每天要往返两次。照这样计算,亮亮一天要走多少千米？

答案： 解析：本题考查小数乘整数的计算及应用。
亮亮每天往返两次，即每天走4段1.3千米的路程。
根据路程=单程距离×走的次数，
可得：
1.3×4=5.2（千米）
答案：5.2千米。

7.为了鼓励市民节约用电,某市电力公司规定了以下电费标准：每月用电不超过60千瓦时,按每千瓦时0.52元收费；每月用电超过60千瓦时,超过的部分按每千瓦时0.6元收费。小明家9月用电90千瓦时,应该缴纳电费多少元？

答案： 解析：本题考查的是分段计费问题，需要先判断用电量是否超过60千瓦时，再根据不同的计费标准计算电费。
答案：小明家9月用电90千瓦时，其中前60千瓦时按每千瓦时0.52元收费，超过的30千瓦时按每千瓦时0.6元收费。
前60千瓦时的费用：$60 × 0.52 = 31.2$（元），
超过60千瓦时的费用：$30 × 0.6 = 18$（元），
总费用：$31.2 + 18 = 49.2$（元）。
答：小明家9月应缴纳电费49.2元。

8.一杯果汁的原价为2.5元,周末开展“买4赠1”促销活动。王老师要给全班45名同学每人买一杯,至少花多少钱？

答案： 解析：本题考查的知识点是小数乘整数的实际应用。我们可以先算出按“买4赠1”一组有多少杯果汁，再算出45名同学需要买几组，最后算出总花费。
步骤一：计算“买4赠1”一组有多少杯果汁
“买4赠1”表示花买4杯果汁的钱可以得到$4 + 1 = 5$杯果汁。
步骤二：计算45名同学需要买几组
$45÷5 = 9$（组），即45名同学刚好可以分成9组。
步骤三：计算每组的花费
每组有4杯是需要付钱的，每杯果汁原价2.5元，根据“总价 = 单价×数量”，可得每组的花费为$2.5×4 = 10$元。
步骤四：计算9组的总花费
已知每组花费10元，一共9组，那么总花费为$10×9 = 90$元。
答案：$2.5×4×(45÷(4 + 1)) = 10×9 = 90$（元），答：至少花90元。