第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 不计算,判断下列各式的积是几位小数。(将小数位数写在括号里。)
3.23×8 (
0.63×0.09(
3.5×0.013(
3.23×8 (
2
) 1.29×0.28(4
)0.63×0.09(
4
) 0.08×1.6(3
)3.5×0.013(
4
) 12.8×0.7(2
)
答案:
1. $3.23×8$($2$)
2. $1.29×0.28$($4$)
3. $0.63×0.09$($4$)
4. $0.08×1.6$($3$)
5. $3.5×0.013$($4$)
6. $12.8×0.7$($2$)
2. $1.29×0.28$($4$)
3. $0.63×0.09$($4$)
4. $0.08×1.6$($3$)
5. $3.5×0.013$($4$)
6. $12.8×0.7$($2$)
2. 一块长方形手帕长 40 厘米、宽 20 厘米。这块手帕的周长是(
1.2
)米,面积是(0.08
)平方米。
答案:
解析:
本题考查长方形的周长和面积计算,以及单位换算。
首先,根据长方形的周长公式:
周长 $= 2 ×$ (长 $+$ 宽)
代入题目中给定的长和宽的值:
周长 $= 2 × (40 + 20) = 120$ (厘米)
由于题目要求把周长换算成米,根据$1米 = 100厘米$,所以:
周长 $= 120 ÷ 100 = 1.2$ (米)
接着,根据长方形的面积公式:
面积 $=$ 长 $×$ 宽
代入题目中给定的长和宽的值:
面积 $= 40 × 20 = 800$ (平方厘米)
由于题目要求把面积换算成平方米,根据$1平方米 = 10000平方厘米$,所以:
面积 $= 800 ÷ 10000 = 0.08$ (平方米)
答案:
这块手帕的周长是$1.2$米,面积是$0.08$平方米。
本题考查长方形的周长和面积计算,以及单位换算。
首先,根据长方形的周长公式:
周长 $= 2 ×$ (长 $+$ 宽)
代入题目中给定的长和宽的值:
周长 $= 2 × (40 + 20) = 120$ (厘米)
由于题目要求把周长换算成米,根据$1米 = 100厘米$,所以:
周长 $= 120 ÷ 100 = 1.2$ (米)
接着,根据长方形的面积公式:
面积 $=$ 长 $×$ 宽
代入题目中给定的长和宽的值:
面积 $= 40 × 20 = 800$ (平方厘米)
由于题目要求把面积换算成平方米,根据$1平方米 = 10000平方厘米$,所以:
面积 $= 800 ÷ 10000 = 0.08$ (平方米)
答案:
这块手帕的周长是$1.2$米,面积是$0.08$平方米。
3. 在一个乘法算式中,一个因数是 0.2,另一个因数是 0.05,积是(
0.01
)。
答案:
解析:题目考查小数乘小数的知识点。小数乘小数,先按照整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
答案:$0.2×0.05 = 0.01$
答案:$0.2×0.05 = 0.01$
4. 用竖式计算。
0.5×0.48 =
0.024×1.8 =
0.34×0.05 =
0.058×0.06 =
0.5×0.48 =
0.24
0.024×1.8 =
0.0432
0.34×0.05 =
0.017
0.058×0.06 =
0.00348
答案:
```
0.5×0.48=0.24
0.48
× 0.5
------
0.240
0.024×1.8=0.0432
0.024
× 1.8
------
0.192
0.024
------
0.0432
0.34×0.05=0.017
0.34
×0.05
------
0.0170
0.058×0.06=0.00348
0.058
×0.06
------
0.00348
```
0.5×0.48=0.24
0.48
× 0.5
------
0.240
0.024×1.8=0.0432
0.024
× 1.8
------
0.192
0.024
------
0.0432
0.34×0.05=0.017
0.34
×0.05
------
0.0170
0.058×0.06=0.00348
0.058
×0.06
------
0.00348
```
(1)与0.488×1.5的积相同的算式是(
A.4.88×1.5
B.15×0.0488
C.48.8×0.15
B
)。A.4.88×1.5
B.15×0.0488
C.48.8×0.15
答案:
解析:本题考查小数乘法的规律,即积的变化规律。根据积的变化规律,一个因数扩大(或缩小)若干倍($0$除外),另一个因数缩小(或扩大)相同的倍数,积不变。
A选项:$4.88$相比较$0.488$,扩大了$10$倍,$1.5$没变,则积扩大了$10$倍,A选项错误。
B选项:$15$相比较$1.5$,扩大了$10$倍,$0.0488$相比较$0.488$,缩小了$10$倍,则积不变,B选项正确。
C选项:$48.8$相比较$0.488$,扩大了$100$倍,$0.15$相比较$1.5$,缩小了$10$倍,则积扩大了$10$倍,C选项错误。
答案:B。
A选项:$4.88$相比较$0.488$,扩大了$10$倍,$1.5$没变,则积扩大了$10$倍,A选项错误。
B选项:$15$相比较$1.5$,扩大了$10$倍,$0.0488$相比较$0.488$,缩小了$10$倍,则积不变,B选项正确。
C选项:$48.8$相比较$0.488$,扩大了$100$倍,$0.15$相比较$1.5$,缩小了$10$倍,则积扩大了$10$倍,C选项错误。
答案:B。
(2)计算5.5+4.5×0.2的结果是(
A.20
B.2
C.5.59
D.6.4
D
)。A.20
B.2
C.5.59
D.6.4
答案:
解析:本题考查小数的四则运算顺序,在没有括号的算式里,如果既有乘除法又有加减法,要先算乘除法,后算加减法。
按照运算顺序,先计算乘法部分:$4.5×0.2 = 0.9$,
再计算加法部分:$5.5 + 0.9 = 6.4$。
答案:D。
按照运算顺序,先计算乘法部分:$4.5×0.2 = 0.9$,
再计算加法部分:$5.5 + 0.9 = 6.4$。
答案:D。
(3)两个数的积由2125变为21.25,其中一个因数不变,另一个因数应(
A.缩小到原来的$\frac{1}{100}$
B.扩大到原来的100倍
C.不变
A
)。A.缩小到原来的$\frac{1}{100}$
B.扩大到原来的100倍
C.不变
答案:
解析:本题可根据积的变化规律来求解。积的变化规律为:在乘法算式中,一个因数不变,另一个因数扩大或缩小若干倍($0$除外),积就扩大或缩小相同的倍数。
已知两个数的积由$2125$变为$21.25$,$2125÷21.25 = 100$,即积缩小到原来的$\frac{1}{100}$。
因为其中一个因数不变,根据积的变化规律可知,另一个因数应缩小到原来的$\frac{1}{100}$。
答案:A。
已知两个数的积由$2125$变为$21.25$,$2125÷21.25 = 100$,即积缩小到原来的$\frac{1}{100}$。
因为其中一个因数不变,根据积的变化规律可知,另一个因数应缩小到原来的$\frac{1}{100}$。
答案:A。
6. 猕猴桃每千克含糖0.08~0.14千克。
(1)0.6千克猕猴桃至少含糖多少千克?
(2)0.5千克猕猴桃最多含糖多少千克?
(1)0.6千克猕猴桃至少含糖多少千克?
(2)0.5千克猕猴桃最多含糖多少千克?
答案:
解析:本题可根据小数乘法的意义,结合题目中给出的每千克猕猴桃含糖量的范围,分别计算出相应重量猕猴桃的含糖量。
(1)求$0.6$千克猕猴桃至少含糖多少千克,因为每千克猕猴桃至少含糖$0.08$千克,所以用每千克至少含糖量乘以猕猴桃的重量即可。
(2)求$0.5$千克猕猴桃最多含糖多少千克,因为每千克猕猴桃最多含糖$0.14$千克,所以用每千克最多含糖量乘以猕猴桃的重量即可。
答案:
(1)$0.08×0.6 = 0.048$(千克)
答:$0.6$千克猕猴桃至少含糖$0.048$千克。
(2)$0.14×0.5 = 0.07$(千克)
答:$0.5$千克猕猴桃最多含糖$0.07$千克。
(1)求$0.6$千克猕猴桃至少含糖多少千克,因为每千克猕猴桃至少含糖$0.08$千克,所以用每千克至少含糖量乘以猕猴桃的重量即可。
(2)求$0.5$千克猕猴桃最多含糖多少千克,因为每千克猕猴桃最多含糖$0.14$千克,所以用每千克最多含糖量乘以猕猴桃的重量即可。
答案:
(1)$0.08×0.6 = 0.048$(千克)
答:$0.6$千克猕猴桃至少含糖$0.048$千克。
(2)$0.14×0.5 = 0.07$(千克)
答:$0.5$千克猕猴桃最多含糖$0.07$千克。
7. 乐乐家9月用水6.8方,用电136.5度。每度电需0.42元,每方水需3.5元。请你算一算:他家9月应缴纳水费、电费分别多少元?
答案:
解析:本题考查小数乘法的实际应用。
水费计算:
用水量:6.8方,
每方水的价格:3.5元,
水费:$6.8 × 3.5 = 23.8$(元),
电费计算:
用电量:136.5度,
每度电的价格:0.42元,
电费:$136.5 × 0.42 = 57.33$(元),
答案:
水费:23.8元,
电费:57.33元。
水费计算:
用水量:6.8方,
每方水的价格:3.5元,
水费:$6.8 × 3.5 = 23.8$(元),
电费计算:
用电量:136.5度,
每度电的价格:0.42元,
电费:$136.5 × 0.42 = 57.33$(元),
答案:
水费:23.8元,
电费:57.33元。
8. 计算:$\underbrace{0.00……00}_{100个"0"}2×\underbrace{0.00……00}_{80个"0"}48= $
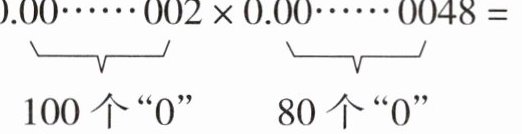
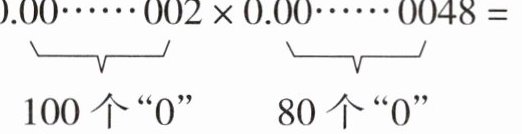
答案:
解析:本题考查小数乘法中积的小数位数的确定方法,先按照整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
两个因数中一共有$100 + 1+80 + 2=183$(位)小数,则积是183位小数。
又因为$2×48 = 96$,所以积的末尾没有$0$。
$\underbrace{0.00……00}_{100个"0"}2×\underbrace{0.00……00}_{80个"0"}48=\underbrace{0.00……00}_{181个"0"}96$。
答案:$\underbrace{0.00……00}_{181个"0"}96$。
两个因数中一共有$100 + 1+80 + 2=183$(位)小数,则积是183位小数。
又因为$2×48 = 96$,所以积的末尾没有$0$。
$\underbrace{0.00……00}_{100个"0"}2×\underbrace{0.00……00}_{80个"0"}48=\underbrace{0.00……00}_{181个"0"}96$。
答案:$\underbrace{0.00……00}_{181个"0"}96$。
9. 在“□”里填上合适的数。
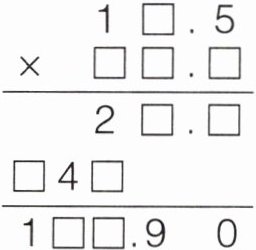

答案:
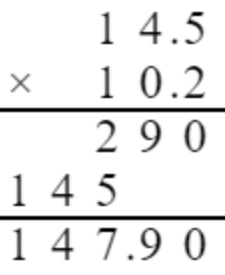
查看更多完整答案,请扫码查看


