《2025年鲁人泰斗假期好时光八年级数学青岛版》

16. (10 分)已知一个正方体的体积是$1000cm^{3}$,现在要在它的$8个角上分别截去8$个大小相同的小正方体,使截去后余下的体积是$488cm^{3}$,问截得的每个小正方体的棱长是多少？

答案： 解：设截得的每个小正方体的棱长为 $ x \, \text{cm} $.
依题意，得 $ 1000 - 8x^{3} = 488 $.
$\therefore 8x^{3} = 512$.
$\therefore x^{3} = 64$.
$\therefore x = 4$.
答：截得的每个小正方体的棱长是 $ 4 \, \text{cm} $.

17. (10 分)已知$2a - 1的平方根是\pm3$,$3a + b - 1的立方根是2$,求$2a - b$的平方根.

答案： 解：
∵2a - 1的平方根是±3，
∴2a - 1 = 9，
解得a = 5。
∵3a + b - 1的立方根是2，
∴3a + b - 1 = 8，
将a = 5代入得：3×5 + b - 1 = 8，
15 + b - 1 = 8，
b = 8 - 15 + 1，
解得b = -6。
∴2a - b = 2×5 - (-6) = 10 + 6 = 16，
∴2a - b的平方根是±4。

18. (10 分)为了绿化环境,我县某中学有一块四边形的空地$ABCD$,如图所示,学校计划在空地上种植草皮,经测量,$\angle ADC = 90^{\circ}$,$CD = 3$米,$AD = 4$米,$AB = 13$米,$BC = 12$米.
(1)求出空地$ABCD$的面积；
(2)若每种植$1平方米草皮需要200$元,问总共需投入多少元？

答案：
解：
(1) 如图，连接 $ AC $，

在 $ \text{Rt} \triangle ACD $ 中，$ AC^{2} = CD^{2} + AD^{2} = 3^{2} + 4^{2} = 5^{2} $，在 $ \triangle ABC $ 中，$ AB^{2} = 13^{2} $，$ BC^{2} = 12^{2} $，而 $ 5^{2} + 12^{2} = 13^{2} $，即 $ AC^{2} + BC^{2} = AB^{2} $，$ \therefore \angle ACB = 90^{\circ} $. $ S_{\text{四边形}ABCD} = S_{\triangle ACB} - S_{\triangle ACD} = \frac{1}{2}AC \cdot BC - \frac{1}{2}AD \cdot CD $ $ = \frac{1}{2} × 5 × 12 - \frac{1}{2} × 4 × 3 = 24(\text{m}^{2}) $.
(2) $ 24 × 200 = 4800 $（元）. 答：总共需投入 $ 4800 $ 元.

19. (10 分)已知$\triangle ABC$中,$AB = AC$,$CD\perp AB于点D$.
(1)若$\angle A = 36^{\circ}$,求$\angle DCB$的度数；(18°)
(2)若$AB = 10$,$CD = 6$,求$BC$的长.($2\sqrt{10}$)

答案： 解：
(1) 在 $ \triangle ABC $ 中，$ \because AB = AC $，$ \angle A = 36^{\circ} $，$ \therefore \angle B = \angle ACB = \frac{180^{\circ} - 36^{\circ}}{2} = 72^{\circ} $. $ \because CD \perp AB $ 于点 $ D $，$ \therefore \angle DCB = 90^{\circ} - 72^{\circ} = 18^{\circ} $.
(2) $ \because \triangle ABC $ 中，$ AB = AC $，$ CD \perp AB $ 于点 $ D $，$ AB = 10 $，$ CD = 6 $，$ \therefore AC = AB = 10 $. 设 $ BD = x $，则 $ AD = 10 - x $，在 $ \text{Rt} \triangle ACD $ 中，$ \because AC^{2} = CD^{2} + AD^{2} $，即 $ 10^{2} = 6^{2} + (10 - x)^{2} $，解得 $ x = 2 $. 在 $ \text{Rt} \triangle BCD $ 中，$ \because BC^{2} = CD^{2} + BD^{2} $，即 $ BC^{2} = 6^{2} + 2^{2} = 40 $，$ \therefore BC = \sqrt{40} = 2\sqrt{10} $.

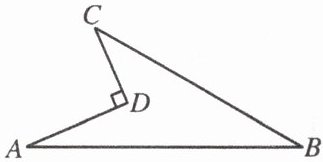
20. (10 分)拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路$AB由点A向点B$行驶,已知点$C$为一所学校,且点$C与直线AB上两点A$,$B的距离分别为150m和200m$,且$AB = 250m$,拖拉机周围$130m$以内为受噪声影响区域.
(1)学校$C$会受噪声影响吗？为什么？
(2)若拖拉机的行驶速度为每分钟$50$米,拖拉机噪声影响该学校持续的时间有多少分钟？

答案：
解：
(1) 学校 $ C $ 会受噪声影响. 理由：如图，过点 $ C $ 作 $ CD \perp AB $ 于点 $ D $，

$ \because AC = 150 \, \text{m} $，$ BC = 200 \, \text{m} $，$ AB = 250 \, \text{m} $，$ \therefore AC^{2} + BC^{2} = AB^{2} $. $ \therefore \triangle ABC $ 是直角三角形.
$ \therefore AC × BC = CD × AB $. $ \therefore 150 × 200 = 250 × CD $. $ \therefore CD = \frac{150 × 200}{250} = 120(\text{m}) $. $ \because $ 拖拉机周围 $ 130 \, \text{m} $ 以内为受噪声影响区域，$ \therefore $ 学校 $ C $ 会受噪声影响.
(2) 当 $ EC = 130 \, \text{m} $，$ FC = 130 \, \text{m} $ 时，正好影响 $ C $ 学校，$ \because ED = \sqrt{EC^{2} - CD^{2}} = \sqrt{130^{2} - 120^{2}} = 50(\text{m}) $，$ \therefore EF = 100(\text{m}) $. $ \because $ 拖拉机的行驶速度为每分钟 $ 50 $ 米，$ \therefore 100 ÷ 50 = 2 $（分钟），即拖拉机噪声影响该学校持续的时间有 $ 2 $ 分钟.