2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是(

B
)
答案:
B
2. 如图,四边形 $ABCD \sim$ 四边形 $EFGH$,$\angle A = 80^{\circ}$,$\angle C = 90^{\circ}$,$\angle F = 70^{\circ}$,则 $\angle E$ 的度数为(
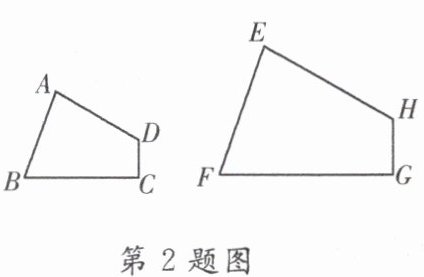
A.$70^{\circ}$
B.$80^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$
B
)
A.$70^{\circ}$
B.$80^{\circ}$
C.$90^{\circ}$
D.$120^{\circ}$
答案:
B
3. 如图,在平面直角坐标系中,已知 $\triangle ABC$ 与 $\triangle DEF$ 是位似图形,原点 $O$ 是位似中心,相似比为 $1:3$,若 $AB = 3$,则 $DE$ 的长为(
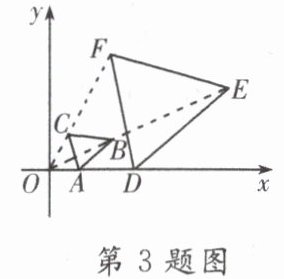
A.5
B.6
C.9
D.12
C
)
A.5
B.6
C.9
D.12
答案:
C【解析】$\because \triangle ABC$与$\triangle DEF$是位似图形,
$\therefore AB// DE$.
$\therefore \triangle OAB\backsim \triangle ODE$.
$\therefore \frac {AB}{DE}=\frac {OA}{OD}$,即$\frac {3}{DE}=\frac {1}{3}$.
解得$DE=9$.故选 C.
$\therefore AB// DE$.
$\therefore \triangle OAB\backsim \triangle ODE$.
$\therefore \frac {AB}{DE}=\frac {OA}{OD}$,即$\frac {3}{DE}=\frac {1}{3}$.
解得$DE=9$.故选 C.
4. 如图,在 $\triangle ABC$ 中,点 $D$ 为 $AC$ 边上一点,$\angle DBC = \angle A$,$BC = \sqrt{6}$,$AC = 3$,则 $CD$ 的长为(
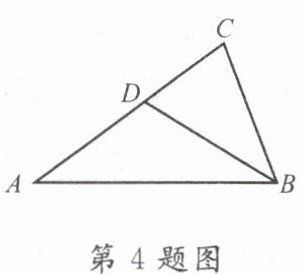
A.1
B.$\frac{3}{2}$
C.2
D.$\frac{5}{2}$
C
)
A.1
B.$\frac{3}{2}$
C.2
D.$\frac{5}{2}$
答案:
C【解析】$\because ∠DBC=∠A,∠C=∠C$,
$\therefore \triangle CBD\backsim \triangle CAB$.
$\therefore \frac {CD}{CB}=\frac {CB}{CA}$,即$\frac {CD}{\sqrt {6}}=\frac {\sqrt {6}}{3}$.
$\therefore CD=2$.故选 C.
$\therefore \triangle CBD\backsim \triangle CAB$.
$\therefore \frac {CD}{CB}=\frac {CB}{CA}$,即$\frac {CD}{\sqrt {6}}=\frac {\sqrt {6}}{3}$.
$\therefore CD=2$.故选 C.
5. 两个相似多边形的一组对应边分别是 $3\mathrm{cm}$ 和 $4.5\mathrm{cm}$,如果它们的周长之和是 $80\mathrm{cm}$,那么较大的多边形的周长是(
A.$16\mathrm{cm}$
B.$32\mathrm{cm}$
C.$48\mathrm{cm}$
D.$52\mathrm{cm}$
C
)A.$16\mathrm{cm}$
B.$32\mathrm{cm}$
C.$48\mathrm{cm}$
D.$52\mathrm{cm}$
答案:
C【解析】设较大多边形与较小多边形的周长分别是$m cm$,$n cm$.则$\frac {n}{m}=\frac {3}{4.5}=\frac {2}{3}$.
因而$n=\frac {2}{3}m$.
根据面积之和是$80cm^{2}$,得到$m+\frac {2}{3}m=80$.
解得$m=48$.
故选 C.
因而$n=\frac {2}{3}m$.
根据面积之和是$80cm^{2}$,得到$m+\frac {2}{3}m=80$.
解得$m=48$.
故选 C.
6. 如图,在 $\triangle ABC$ 中,点 $D$ 是 $AB$ 边上一点,过点 $D$ 作 $DE // BC$ 交 $AC$ 边于点 $E$,点 $N$ 是 $BC$ 边上一点,连接 $AN$ 交 $DE$ 于点 $M$,则下列结论错误的是(
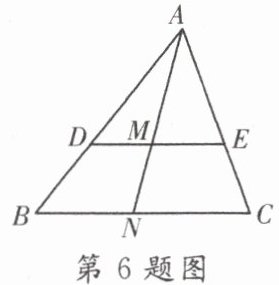
A.$\frac{AM}{AN} = \frac{ME}{CN}$
B.$\frac{AD}{BD} = \frac{AE}{CE}$
C.$\frac{DM}{BN} = \frac{EM}{CN}$
D.$\frac{BD}{AB} = \frac{DM}{BN}$
D
)
A.$\frac{AM}{AN} = \frac{ME}{CN}$
B.$\frac{AD}{BD} = \frac{AE}{CE}$
C.$\frac{DM}{BN} = \frac{EM}{CN}$
D.$\frac{BD}{AB} = \frac{DM}{BN}$
答案:
D【解析】$\because DE// BC$,
$\therefore \frac {AD}{BD}=\frac {AE}{EC},\triangle ADM\backsim \triangle ABN,\triangle AME\backsim \triangle ANC$.
$\therefore \frac {AM}{AN}=\frac {ME}{NC},\frac {DM}{BN}=\frac {AM}{AN}=\frac {AD}{AB}$.
$\therefore \frac {DM}{BN}=\frac {EM}{CN}$.故选 D.
$\therefore \frac {AD}{BD}=\frac {AE}{EC},\triangle ADM\backsim \triangle ABN,\triangle AME\backsim \triangle ANC$.
$\therefore \frac {AM}{AN}=\frac {ME}{NC},\frac {DM}{BN}=\frac {AM}{AN}=\frac {AD}{AB}$.
$\therefore \frac {DM}{BN}=\frac {EM}{CN}$.故选 D.
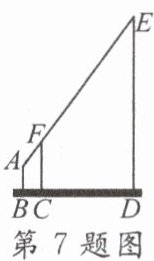
7. 如图,某测量工作人员站在地面点 $B$ 处利用标杆 $FC$ 测量一旗杆 $ED$ 的高度. 测量人员眼睛处点 $A$ 与标杆顶端处点 $F$,旗杆顶端处点 $E$ 在同一直线上,点 $B$,$C$,$D$ 也在同一条直线上. 已知此人眼睛到地面距离 $AB = 1.6$ 米,标杆高 $FC = 3.2$ 米,且 $BC = 1$ 米,$CD = 5$ 米,则旗杆的高度为( )
A.$8.4$ 米
B.$9.6$ 米
C.$11.2$ 米
D.$12.4$ 米

A.$8.4$ 米
B.$9.6$ 米
C.$11.2$ 米
D.$12.4$ 米
答案:
C【解析】作$AH⊥ED$交$FC$于点$G$,
如图所示,

$\because FC⊥BD,ED⊥BD,AH⊥ED$,
$\therefore FG// EH$.
$\because AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC$,
$\therefore AH=BD,AG=BC$.
$\because AB=1.6,FC=3.2,BC=1,CD=5$,
$\therefore FG=3.2 - 1.6 = 1.6,BD=6$.
$\because FG// EH$,
$\therefore \frac {FG}{EH}=\frac {AG}{AH},\frac {1.6}{EH}=\frac {1}{6}$.
解得$EH=9.6$.
$\therefore ED=9.6 + 1.6 = 11.2(m)$
$\therefore$ 旗杆的高度为$11.2$米.故选 C.
C【解析】作$AH⊥ED$交$FC$于点$G$,
如图所示,

$\because FC⊥BD,ED⊥BD,AH⊥ED$,
$\therefore FG// EH$.
$\because AH⊥ED,BD⊥ED,AB⊥BC,ED⊥BC$,
$\therefore AH=BD,AG=BC$.
$\because AB=1.6,FC=3.2,BC=1,CD=5$,
$\therefore FG=3.2 - 1.6 = 1.6,BD=6$.
$\because FG// EH$,
$\therefore \frac {FG}{EH}=\frac {AG}{AH},\frac {1.6}{EH}=\frac {1}{6}$.
解得$EH=9.6$.
$\therefore ED=9.6 + 1.6 = 11.2(m)$
$\therefore$ 旗杆的高度为$11.2$米.故选 C.
8. 在平面直角坐标系中,矩形 $OABC$ 的顶点坐标分别是 $O(0,0)$,$A(8,0)$,$B(8,6)$,$C(0,6)$. 已知矩形 $OA_1B_1C_1$ 与矩形 $OABC$ 位似,位似中心是原点 $O$,且矩形 $OA_1B_1C_1$ 的面积等于矩形 $OABC$ 面积的 $\frac{1}{2}$,则点 $B_1$ 的坐标为(
A.$(4,3)$
B.$(4,3)$ 或 $(-4,-3)$
C.$(4\sqrt{2},3\sqrt{2})$
D.$(4\sqrt{2},3\sqrt{2})$ 或 $(-4\sqrt{2},-3\sqrt{2})$
D
)A.$(4,3)$
B.$(4,3)$ 或 $(-4,-3)$
C.$(4\sqrt{2},3\sqrt{2})$
D.$(4\sqrt{2},3\sqrt{2})$ 或 $(-4\sqrt{2},-3\sqrt{2})$
答案:
D【解析】$\because$ 矩形$OA_{1}B_{1}C_{1}$与矩形$OABC$位似,矩形$OA_{1}B_{1}C_{1}$的面积等于矩形$OABC$面积的$\frac {1}{2}$,
$\therefore$ 矩形$OA_{1}B_{1}C_{1}$与矩形$OABC$的相似比为$1:\sqrt {2}$.
$\because$ 矩形$OA_{1}B_{1}C_{1}$与矩形$OABC$位似,位似中心是原点$O$,点$B$的坐标为$(8,6)$,
$\therefore$ 点$B_{1}$的坐标为$(8×\frac {\sqrt {2}}{2},6×\frac {\sqrt {2}}{2})$或$(-8×\frac {\sqrt {2}}{2},-6×\frac {\sqrt {2}}{2})$,即$(4\sqrt {2},3\sqrt {2})$或$(-4\sqrt {2},-3\sqrt {2})$.故选 D.
$\therefore$ 矩形$OA_{1}B_{1}C_{1}$与矩形$OABC$的相似比为$1:\sqrt {2}$.
$\because$ 矩形$OA_{1}B_{1}C_{1}$与矩形$OABC$位似,位似中心是原点$O$,点$B$的坐标为$(8,6)$,
$\therefore$ 点$B_{1}$的坐标为$(8×\frac {\sqrt {2}}{2},6×\frac {\sqrt {2}}{2})$或$(-8×\frac {\sqrt {2}}{2},-6×\frac {\sqrt {2}}{2})$,即$(4\sqrt {2},3\sqrt {2})$或$(-4\sqrt {2},-3\sqrt {2})$.故选 D.
查看更多完整答案,请扫码查看


