《2025年鲁人泰斗假期好时光八年级数学青岛版》

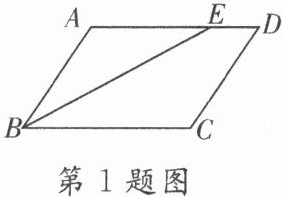
1. 如图,在$□ ABCD$中,$AB = 3$,$BC = 5$,$\angle ABC的平分线交AD于点E$,则$DE$的长为(D)

A.5
B.4
C.3
D.2

答案： D

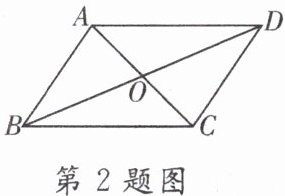
2. 如图,在$□ ABCD$中,不一定成立的是(D)
①$AO = CO$；②$AC\perp BD$；③$AD// BC$；④$\angle CAB = \angle CAD$。

A.①和④
B.②和③
C.③和④
D.②和④

答案： D

3. 若平行四边形的两条对角线长为$6cm和16cm$,则下列长度的线段可作为平行四边形边长的是(B)
A.$5cm$
B.$8cm$
C.$12cm$
D.$16cm$

答案： B

4. 如图,在$□ ABCD$中,点$E是AB$边中点,$DE与CB的延长线交于点F$。求证：$DE = FE$。
证明：∵ 四边形ABCD是平行四边形，
∴ AD//BC.
又 ∵ 点F在CB的延长线上，
∴ AD//CF.
∴ ∠ADE = ∠F.
∵ 点E是AB边的中点，
∴ AE = BE.
在 △ADE 与 △BFE 中，
{∠ADE = ∠F,
∠AED = ∠BEF,
AE = BE,
∴ △ADE ≌ △BFE(AAS).
∴ DE = FE.

答案： 证明：
∵ 四边形ABCD是平行四边形，
∴ AD//BC.
又
∵ 点F在CB的延长线上，
∴ AD//CF.
∴ ∠ADE = ∠F.
∵ 点E是AB边的中点，
∴ AE = BE.
在 △ADE 与 △BFE 中，
{∠ADE = ∠F,
∠AED = ∠BEF,
AE = BE,
∴ △ADE ≌ △BFE(AAS).
∴ DE = FE.

5. 能判定四边形$ABCD$为平行四边形的题设是(C)
A.$AB// CD$,$AD = BC$
B.$\angle A = \angle B$,$\angle C = \angle D$
C.$AB = CD$,$AD = BC$
D.$AB = AD$,$CB = CD$

答案： C

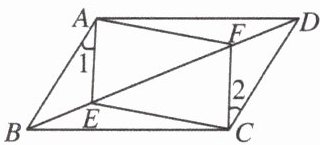
6. 如图,在$□ ABCD$中,$E$,$F是对角线BD$上的两点,如果添加一个条件使四边形$AECF$是平行四边形,则添加的条件不能是(A)

A.$AE = CF$
B.$BE = FD$
C.$BF = DE$
D.$\angle 1 = \angle 2$

答案： A 【解析】
∵ 四边形ABCD是平行四边形，
∴ AB = CD，∠ABD = ∠CDB.
又
∵ BE = DF，
∴ △ABE ≌ △CDF(SAS).
∴ AE = CF，∠AEB = ∠CFD.
∴ ∠AEF = ∠CFE.
∴ AE//CF.
∴ 四边形AECF是平行四边形，故B正确；
∵ 四边形ABCD是平行四边形，
∴ AB = CD，∠ABD = ∠CDB.
又
∵ BF = DE，
∴ BF - EF = DE - EF.
∴ BE = DF.
∴ △ABE ≌ △CDF(SAS).
∴ AE = CF，∠AEB = ∠CFD.
∴ ∠AEF = ∠CFE.
∴ AE//CF.
∴ 四边形AECF是平行四边形，故C正确；
∵ 四边形ABCD是平行四边形，
∴ AB = CD，∠ABD = ∠CDB.
又
∵ ∠1 = ∠2，
∴ △ABE ≌ △CDF(ASA).
∴ AE = CF，∠AEB = ∠CFD.
∴ ∠AEF = ∠CFE.
∴ AE//CF.
∴ 四边形AECF是平行四边形，故D正确；
添加AE = CF后，不能得出 △ABE ≌ △CDF，进而得不出四边形AECF是平行四边形. 故选A.

7. 如图,在$□ ABCD$中,点$E$,$F分别在BC$,$AD$上,$AC与EF相交于点O$,且$AO = CO$。求证：四边形$AECF$是平行四边形。
证明：∵ 四边形ABCD是平行四边形，
∴ AD//BC.
∴ ∠OAF = ∠OCE.
在 △AOF 和 △COE 中，
{∠OAF = ∠OCE,
AO = CO,
∠AOF = ∠COE,
∴ △AOF ≌ △COE(ASA).
∴ FO = EO.
又 ∵ AO = CO，
∴ 四边形AECF是平行四边形.

答案： 证明：
∵ 四边形ABCD是平行四边形，
∴ AD//BC.
∴ ∠OAF = ∠OCE.
在 △AOF 和 △COE 中，
{∠OAF = ∠OCE,
AO = CO,
∠AOF = ∠COE,
∴ △AOF ≌ △COE(ASA).
∴ FO = EO.
又
∵ AO = CO，
∴ 四边形AECF是平行四边形.

8. 下列结论中,菱形具有而矩形不一定具有的性质是(C)
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对边相等且平行

答案： C 【解析】A.
∵ 矩形的对角线相等，
∴ 此选项不符合题意；
B.
∵ 矩形和菱形的对角线都互相平分，
∴ 此选项不符合题意；C.
∵ 菱形对角线互相垂直，矩形的对角线不一定互相垂直，
∴ 此选项符合题意；D.
∵ 矩形和菱形的对边都相等且平行，
∴ 此选项不符合题意. 故选C.