2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在$8×8$的网格中,每个小正方形的顶点叫做格点,$\triangle OAB$的顶点都在格点上,请在网格中画出$\triangle OAB$的一个位似图形,使两个图形以 O 为位似中心,且所画图形与$\triangle OAB的位似比为2:1$。
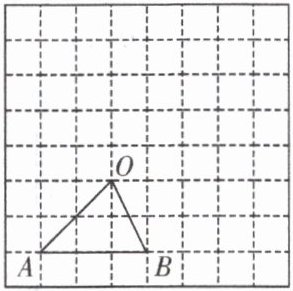

答案:
解: 如图所示, $\triangle A'OB'$ 即为所求.

解: 如图所示, $\triangle A'OB'$ 即为所求.

2. 如图,在$10×10$的正方形网格中,点 A,B,C,D 均在格点上,以点 A 为位似中心画四边形$AB'C'D'$,使它与四边形 ABCD 位似,且相似比为 2。
(1)在图中画出四边形$AB'C'D'$;
(2)$\triangle AC'D'$是什么三角形?
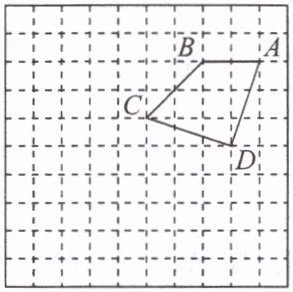
(1)在图中画出四边形$AB'C'D'$;
(2)$\triangle AC'D'$是什么三角形?

答案:
解:
(1) 如图所示, 四边形 $AB'C'D'$ 即为所求.

(2)
∵$AC'^2 = 4^2 + 8^2 = 16 + 64 = 80$, $AD'^2 = 6^2 + 2^2 = 36 + 4 = 40$, $C'D'^2 = 6^2 + 2^2 = 36 + 4 = 40$,
∴$AD' = C'D'$, $AD'^2 + C'D'^2 = AC'^2$.
∴$\triangle AC'D'$ 是等腰直角三角形.
解:
(1) 如图所示, 四边形 $AB'C'D'$ 即为所求.

(2)
∵$AC'^2 = 4^2 + 8^2 = 16 + 64 = 80$, $AD'^2 = 6^2 + 2^2 = 36 + 4 = 40$, $C'D'^2 = 6^2 + 2^2 = 36 + 4 = 40$,
∴$AD' = C'D'$, $AD'^2 + C'D'^2 = AC'^2$.
∴$\triangle AC'D'$ 是等腰直角三角形.
3. 如图,在$6×6$的正方形网格中,每个小正方形的边长都是 1,我们把顶点都在格点上的三角形叫做格点三角形,例如$\triangle ABC$是一个格点三角形。
(1)在图①中,请判断$\triangle ABC与\triangle DEF$是否相似,并说明理由;
(2)在图②中,以点 O 为位似中心,再画一个格点三角形,使它与$\triangle ABC的位似比为2:1$。
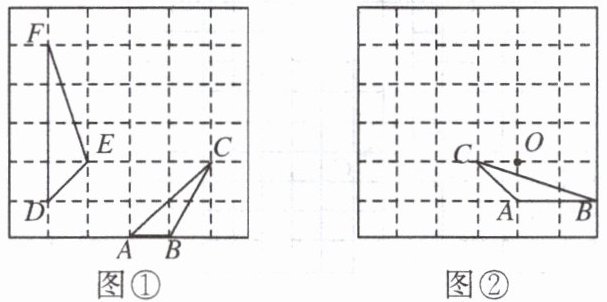
(1)在图①中,请判断$\triangle ABC与\triangle DEF$是否相似,并说明理由;
(2)在图②中,以点 O 为位似中心,再画一个格点三角形,使它与$\triangle ABC的位似比为2:1$。

答案:
解:
(1) 相似. 理由如下:
∵$AB = 1$, $BC = \sqrt{1^2 + 2^2} = \sqrt{5}$, $AC = \sqrt{2^2 + 2^2} = 2\sqrt{2}$,
$DE = \sqrt{1^2 + 1^2} = \sqrt{2}$, $EF = \sqrt{1^2 + 3^2} = \sqrt{10}$, $DF = 4$,
∴$\frac{AB}{DE} = \frac{1}{\sqrt{2}}$, $\frac{BC}{EF} = \frac{\sqrt{5}}{\sqrt{10}} = \frac{1}{\sqrt{2}}$, $\frac{AC}{DF} = \frac{2\sqrt{2}}{4} = \frac{1}{\sqrt{2}}$.
∴$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$.
∴$\triangle ABC \backsim \triangle DEF$.
(2) 如图②, $\triangle A_1B_1C_1$ 即为所作.

解:
(1) 相似. 理由如下:
∵$AB = 1$, $BC = \sqrt{1^2 + 2^2} = \sqrt{5}$, $AC = \sqrt{2^2 + 2^2} = 2\sqrt{2}$,
$DE = \sqrt{1^2 + 1^2} = \sqrt{2}$, $EF = \sqrt{1^2 + 3^2} = \sqrt{10}$, $DF = 4$,
∴$\frac{AB}{DE} = \frac{1}{\sqrt{2}}$, $\frac{BC}{EF} = \frac{\sqrt{5}}{\sqrt{10}} = \frac{1}{\sqrt{2}}$, $\frac{AC}{DF} = \frac{2\sqrt{2}}{4} = \frac{1}{\sqrt{2}}$.
∴$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$.
∴$\triangle ABC \backsim \triangle DEF$.
(2) 如图②, $\triangle A_1B_1C_1$ 即为所作.

1. 如果多边形有一个顶点在坐标原点,有一条边在 x 轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得的图形与原图形是
位似图形
,坐标原点
是它们的位似中心。
答案:
位似图形 坐标原点
2. 在直角坐标系中,将一个多边形每个顶点的横坐标、纵坐标都乘同一个数$k(k≠0,1)$,所对应的图形与原图形位似,位似中心是
坐标原点
,它们的相似比为|k|
。
答案:
坐标原点 $|k|$
【典型例题 4】如图,$\triangle ABO三个顶点的坐标分别为A(2,4)$,$B(6,0)$,$O(0,0)$,以原点 O 为位似中心,把这个三角形缩小为原来的$\frac{1}{2}$,可以得到$\triangle A'B'O$,已知点$B'的坐标是(3,0)$,则点$A'$的坐标是____
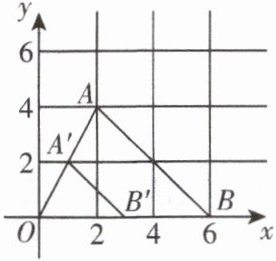
(1,2)
。
答案:
解析:
∵点 A 的坐标为$(2,4)$,以原点 O 为位似中心,把这个三角形缩小为原来的$\frac{1}{2}$,
∴点$A'的坐标是(2×\frac{1}{2},4×\frac{1}{2})$,即$(1,2)$。
答案:$(1,2)$
∵点 A 的坐标为$(2,4)$,以原点 O 为位似中心,把这个三角形缩小为原来的$\frac{1}{2}$,
∴点$A'的坐标是(2×\frac{1}{2},4×\frac{1}{2})$,即$(1,2)$。
答案:$(1,2)$
查看更多完整答案,请扫码查看


