2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,有a,b,c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线(

A.a户最长
B.b户最长
C.c户最长
D.三户一样长
D
)
A.a户最长
B.b户最长
C.c户最长
D.三户一样长
答案:
1.D
2. 线段CD是由线段AB平移得到的,点A(3,-1)的对应点C的坐标是(-2,5),则点B(0,4)的对应点D的坐标是(
A.(5,-7)
B.(4,3)
C.(-5,10)
D.(-3,7)
C
)A.(5,-7)
B.(4,3)
C.(-5,10)
D.(-3,7)
答案:
2.C
3. 将一点A(1,2)向右平移2个单位得到一个对应点A',则点A'的坐标是____
(3,2)
。
答案:
3.(3,2)
4. 将△ABC沿BC的方向平移得到△DEF。
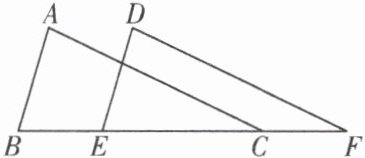
(1)若∠B= 74°,∠F= 26°,求∠A的度数;
(2)若BC= 4.5cm,EC= 3.5cm,求△ABC平移的距离。

(1)若∠B= 74°,∠F= 26°,求∠A的度数;
80°
(2)若BC= 4.5cm,EC= 3.5cm,求△ABC平移的距离。
1cm
答案:
4.解:
(1)由图形平移的特征可知△ABC和△DEF的形状与大小相同,即△ABC≌△DEF,
∴∠ACB=∠F=26°.
∵∠B=74°,
∴∠A=180°−(∠ACB+∠B)=180°−(26°+74°)=80°.
(2)
∵BC = 4.5cm, EC = 3.5cm,
∴BE = BC - EC = 4.5 - 3.5 = 1(cm).
∴△ABC平移的距离为1cm.
(1)由图形平移的特征可知△ABC和△DEF的形状与大小相同,即△ABC≌△DEF,
∴∠ACB=∠F=26°.
∵∠B=74°,
∴∠A=180°−(∠ACB+∠B)=180°−(26°+74°)=80°.
(2)
∵BC = 4.5cm, EC = 3.5cm,
∴BE = BC - EC = 4.5 - 3.5 = 1(cm).
∴△ABC平移的距离为1cm.
5. 如图,在△ABC中,∠BAC= 32°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠C'AB的度数为(
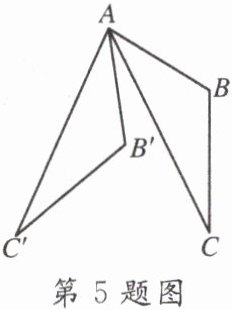
A.18°
B.82°
C.64°
D.100°
B
)
A.18°
B.82°
C.64°
D.100°
答案:
5.B
6. 如图,E,F分别是正方形ABCD的边AB,BC上的点,且BE= CF,连接CE,DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( )
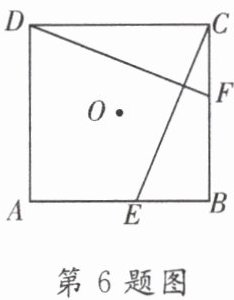
A.30°
B.45°
C.60°
D.90°

A.30°
B.45°
C.60°
D.90°
答案:
6.D [解析]
∵正方形ABCD中,O为正方形的中心,
∴OD =OC,OD⊥OC,
∴∠DOC=90°,由题意得,点D对应点为点C,连接OC,OD,∠DOC即为旋转角,则将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,旋转角为90°.故选D.

6.D [解析]
∵正方形ABCD中,O为正方形的中心,
∴OD =OC,OD⊥OC,
∴∠DOC=90°,由题意得,点D对应点为点C,连接OC,OD,∠DOC即为旋转角,则将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,旋转角为90°.故选D.

7. 方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上。
(1)画出△ABC绕点B顺时针旋转90°后的$△A_1B_1C_1,$并写出点$A_1$的坐标;
(2)画出△ABC关于原点O对称的$△A_2B_2C_2。$
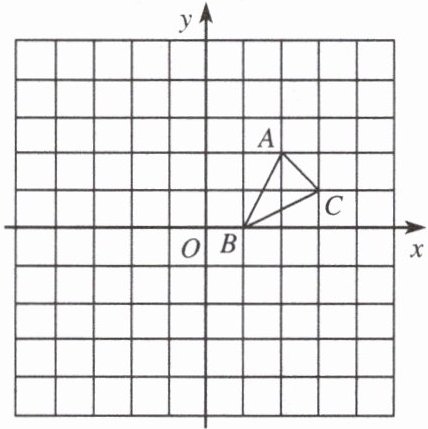
(1)画出△ABC绕点B顺时针旋转90°后的$△A_1B_1C_1,$并写出点$A_1$的坐标;
(2)画出△ABC关于原点O对称的$△A_2B_2C_2。$

答案:
7.解:
(1)如图所示,△A₁B₁C₁即为所求,其中点A₁的坐标为(3,−1).

(2)如图所示,△A₂B₂C₂即为所求.
7.解:
(1)如图所示,△A₁B₁C₁即为所求,其中点A₁的坐标为(3,−1).

(2)如图所示,△A₂B₂C₂即为所求.
8. 如图,在Rt△ABC中,∠ACB= 90°,△DCE是△ABC绕着点C顺时针方向旋转得到的,此时B,C,E在同一直线上。
(1)求旋转角的大小;
(2)若AB= 10,AC= 8,求BE的长。
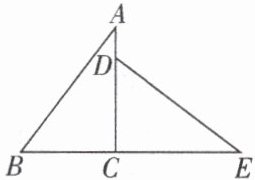
(1)求旋转角的大小;
90°
(2)若AB= 10,AC= 8,求BE的长。
14

答案:
8.解:
(1)
∵△DCE是△ABC绕着点C顺时针方向旋转得到的,此时点B,C,E在同一直线上,
∴∠ACE=90°,即旋转角为90°.
(2)在Rt△ABC中,
∵AB = 10, AC = 8,
∴BC = $\sqrt{AB^2 - AC^2}$ = 6.
∵△ABC绕着点C旋转得到△DCE,
∴△ABC≌△EDC.
∴CE = CA = 8.
∴BE = BC + CE = 6 + 8 = 14.
(1)
∵△DCE是△ABC绕着点C顺时针方向旋转得到的,此时点B,C,E在同一直线上,
∴∠ACE=90°,即旋转角为90°.
(2)在Rt△ABC中,
∵AB = 10, AC = 8,
∴BC = $\sqrt{AB^2 - AC^2}$ = 6.
∵△ABC绕着点C旋转得到△DCE,
∴△ABC≌△EDC.
∴CE = CA = 8.
∴BE = BC + CE = 6 + 8 = 14.
查看更多完整答案,请扫码查看


