2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
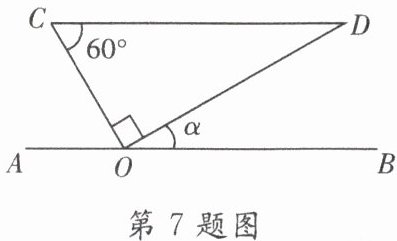
7. 如图, 将三角板的直角顶点放置在直线 $A B$ 的点 $O$ 处, 使斜边 $C D / / A B$, 则 $\angle \alpha$ 的余弦的值是
$\frac{\sqrt{3}}{2}$
.
答案:
7.$\frac{\sqrt{3}}{2}$
8. 如何求$22.5^{\circ}$的正切值, 小明想了一个办法: 把一张正方形纸片 (正方形 $A B C D$ ) 按如图方式折叠, 使顶点 $B$恰好落在对角线 $A C$ 上, 折痕为 $E C$. 根据小明的操作通过计算可以得到$\tan 22.5^{\circ}=$
$\sqrt{2}-1$
. (保留根号)
答案:
8.$\sqrt{2}$−1
9. 计算:
(1) $2 \sin 30^{\circ}-3 \tan 45^{\circ} \cdot \sin 45^{\circ}+4 \cos 60^{\circ}$;
(2) $\frac{\sin 45^{\circ}}{\cos 30^{\circ}-\tan 60^{\circ}}+\cos 45^{\circ} \cdot \sin 60^{\circ}$.
(1) $2 \sin 30^{\circ}-3 \tan 45^{\circ} \cdot \sin 45^{\circ}+4 \cos 60^{\circ}$;
(2) $\frac{\sin 45^{\circ}}{\cos 30^{\circ}-\tan 60^{\circ}}+\cos 45^{\circ} \cdot \sin 60^{\circ}$.
答案:
9.解:
(1)$2 \sin 30^{\circ}-3 \tan 45^{\circ} \cdot \sin 45^{\circ}+4 \cos 60^{\circ}$
$=2×\frac{1}{2}-3×1×\frac{\sqrt{2}}{2}+4×\frac{1}{2}$
$=1-\frac{3\sqrt{2}}{2}+2$
$=3-\frac{3\sqrt{2}}{2}$
(2)$\frac{\sin 45^{\circ}}{\cos 30^{\circ}-\tan 60^{\circ}}+\cos 45^{\circ} \cdot \sin 60^{\circ}$
$=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}-\sqrt{3}}+\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$
$=\frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{3}}{2}}+\frac{\sqrt{6}}{4}$
$=-\frac{\sqrt{2}}{\sqrt{3}}+\frac{\sqrt{6}}{4}$
$=-\frac{\sqrt{6}}{3}+\frac{\sqrt{6}}{4}$
$=-\frac{4\sqrt{6}}{12}+\frac{3\sqrt{6}}{12}$
$=-\frac{\sqrt{6}}{12}$
(1)$2 \sin 30^{\circ}-3 \tan 45^{\circ} \cdot \sin 45^{\circ}+4 \cos 60^{\circ}$
$=2×\frac{1}{2}-3×1×\frac{\sqrt{2}}{2}+4×\frac{1}{2}$
$=1-\frac{3\sqrt{2}}{2}+2$
$=3-\frac{3\sqrt{2}}{2}$
(2)$\frac{\sin 45^{\circ}}{\cos 30^{\circ}-\tan 60^{\circ}}+\cos 45^{\circ} \cdot \sin 60^{\circ}$
$=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}-\sqrt{3}}+\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$
$=\frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{3}}{2}}+\frac{\sqrt{6}}{4}$
$=-\frac{\sqrt{2}}{\sqrt{3}}+\frac{\sqrt{6}}{4}$
$=-\frac{\sqrt{6}}{3}+\frac{\sqrt{6}}{4}$
$=-\frac{4\sqrt{6}}{12}+\frac{3\sqrt{6}}{12}$
$=-\frac{\sqrt{6}}{12}$
10. 已知$\alpha$是锐角, 且$\sin \left(\alpha+15^{\circ}\right)= \frac{\sqrt{3}}{2}$. 计算$\sqrt{8}-4 \cos \alpha-(\pi-3.14)^{0}+\tan \alpha+\left(\frac{1}{3}\right)^{-1}$的值.
答案:
解:
∵α是锐角,且$\sin(\alpha + 15^{\circ}) = \frac{\sqrt{3}}{2}$,
∴$\alpha + 15^{\circ} = 60^{\circ}$,解得$\alpha = 45^{\circ}$。
原式$= \sqrt{8} - 4\cos\alpha - (\pi - 3.14)^0 + \tan\alpha + \left(\frac{1}{3}\right)^{-1}$
$= 2\sqrt{2} - 4×\frac{\sqrt{2}}{2} - 1 + 1 + 3$
$= 2\sqrt{2} - 2\sqrt{2} - 1 + 1 + 3$
$= 3$。
答案:3
∵α是锐角,且$\sin(\alpha + 15^{\circ}) = \frac{\sqrt{3}}{2}$,
∴$\alpha + 15^{\circ} = 60^{\circ}$,解得$\alpha = 45^{\circ}$。
原式$= \sqrt{8} - 4\cos\alpha - (\pi - 3.14)^0 + \tan\alpha + \left(\frac{1}{3}\right)^{-1}$
$= 2\sqrt{2} - 4×\frac{\sqrt{2}}{2} - 1 + 1 + 3$
$= 2\sqrt{2} - 2\sqrt{2} - 1 + 1 + 3$
$= 3$。
答案:3
打开科学计算器,启动开机键后,使显示器上方显示 DEG(如果没有显示 DEG,可以按 DR 1 键),表示计算器已经进入以“
度
”为角的度量单位的运算状态.这时,按相应的三角比的名称键,再输入锐角的度数,按=
键后,显示器显示的数字即为该锐角相应的三角比的值.
答案:
度 =
【典型例题 1】 求下列各组锐角的三角函数值(精确到 0.0001):
(1) $\sin70^{\circ},\sin50^{\circ}35'25'',\sin30.5^{\circ}$;
(2) $\cos20^{\circ},\cos10^{\circ}56',\cos87^{\circ}4'$;
(3) $\tan35^{\circ}24',\tan15^{\circ}40',\tan80^{\circ}42'8''$.
(1) $\sin70^{\circ},\sin50^{\circ}35'25'',\sin30.5^{\circ}$;
(2) $\cos20^{\circ},\cos10^{\circ}56',\cos87^{\circ}4'$;
(3) $\tan35^{\circ}24',\tan15^{\circ}40',\tan80^{\circ}42'8''$.
答案:
思路点拨:根据锐角三角函数的定义以及计算器即可求出答案.
解:
(1) $\sin70^{\circ}\approx0.9397,\sin50^{\circ}35'25''\approx0.7726,\sin30.5^{\circ}\approx0.5075$;
(2) $\cos20^{\circ}\approx0.9397,\cos10^{\circ}56'\approx0.9818,\cos87^{\circ}4'\approx0.0512$;
(3) $\tan35^{\circ}24'\approx0.7107,\tan15^{\circ}40'\approx0.2805,\tan80^{\circ}42'8''\approx6.1081$.
解:
(1) $\sin70^{\circ}\approx0.9397,\sin50^{\circ}35'25''\approx0.7726,\sin30.5^{\circ}\approx0.5075$;
(2) $\cos20^{\circ}\approx0.9397,\cos10^{\circ}56'\approx0.9818,\cos87^{\circ}4'\approx0.0512$;
(3) $\tan35^{\circ}24'\approx0.7107,\tan15^{\circ}40'\approx0.2805,\tan80^{\circ}42'8''\approx6.1081$.
查看更多完整答案,请扫码查看


