《2025年鲁人泰斗假期好时光八年级数学青岛版》

3. 在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,各边都扩大 5 倍,则 $ \tan A $ 的值(A)
A.不变
B.扩大 5 倍
C.缩小 5 倍
D.不能确定

答案： A

4. 如图,在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AB = 13 $,$ AC = 7 $,则 $ \sin B = $______$\frac{7}{13}$.

答案： $\frac{7}{13}$

锐角 $ A $ 的正弦、余弦、正切统称为锐角 $ A $ 的三角比.

答案： 正弦　余弦　正切

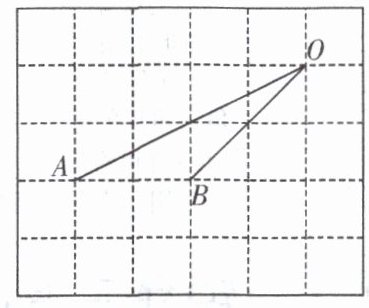
【典型例题 2】如图,在下列网格中,小正方形的边长均为 1,点 $ A $,$ B $,$ O $ 都在格点上,则 $ \angle AOB $ 的正弦值是( )


A.$ \frac{3\sqrt{10}}{10} $
B.$ \frac{1}{2} $
C.$ \frac{1}{3} $
D.$ \frac{\sqrt{10}}{10} $

答案：
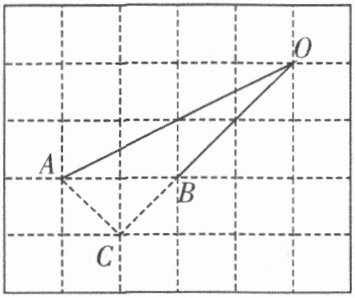
解析：作 $ AC \perp OB $ 于点 $ C $,则 $ AC = \sqrt{2} $,$ AO = \sqrt{2^{2} + 4^{2}} = \sqrt{20} = 2\sqrt{5} $,则 $ \sin \angle AOB = \frac{AC}{AO} = \frac{\sqrt{2}}{2\sqrt{5}} = \frac{\sqrt{10}}{10} $.

答案：D

1. 在 $ Rt\triangle ABC $ 中,$ \angle C = 90^{\circ} $,那么锐角 $ A $ 的正弦等于(B)
A.$ \frac{锐角A的对边}{锐角A的邻边} $
B.$ \frac{锐角A的对边}{斜边} $
C.$ \frac{锐角A的邻边}{斜边} $
D.$ \frac{锐角A的邻边}{锐角A的对边} $

答案： B

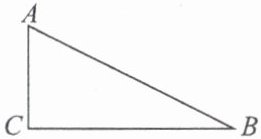
2. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,设 $ \angle A $,$ \angle B $,$ \angle C $ 所对的边分别为 $ a $,$ b $,$ c $,则(C)

A.$ \sin A = \frac{a}{b} $
B.$ a = \sin B × c $
C.$ \cos A = \frac{b}{c} $
D.$ \tan A = \frac{b}{a} $

答案： C　[解析]在△ABC中,∠C = 90°,设∠A,∠B,∠C所对的边分别为a,b,c,因此有$\sin A = \frac{a}{c}$，$\sin B = \frac{b}{c}$，$\cos A = \frac{b}{c}$，$\tan A = \frac{a}{b}$，故A不符合题意，C符合题意，D不符合题意;由$\sin B = \frac{b}{c}$，可得$b = \sin B × c$，故B不符合题意。故选C。

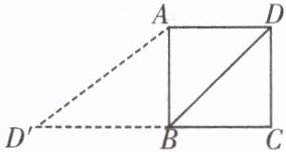
3. 如图,已知正方形 $ ABCD $ 的边长为 2. 如果将线段 $ BD $ 绕着点 $ B $ 旋转后,点 $ D $ 落在 $ CB $ 的延长线上的点 $ D' $ 处,那么 $ \tan \angle BAD' $ 等于$\sqrt{2}$.

答案： $\sqrt{2}$