2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 如图,在$\triangle ABC$中,$BD\perp AC于点D$,$AE\perp BC于点E$,交$BD于点F$,下列三角形中不一定与$\triangle BCD$相似的是(
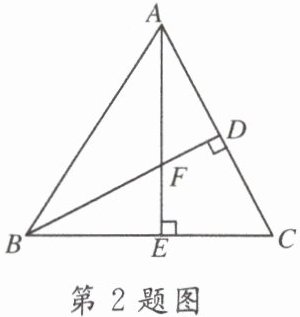
A.$\triangle BFE$
B.$\triangle AFD$
C.$\triangle ACE$
D.$\triangle BAE$
D
)
A.$\triangle BFE$
B.$\triangle AFD$
C.$\triangle ACE$
D.$\triangle BAE$
答案:
2.D [解析]
∵BD⊥AC,AE⊥BC,
∴∠BDC=∠AEC=90°.
∴∠DBC+∠C=∠EAC+∠C=90°.
∴∠DBC=∠EAC.
∴△ACE∽△BCD.
又
∵∠ADF=∠BDC=90°
∴△AFD∽△BCD.
∵∠FBE=∠DBC、∠BEF=∠BDC=90°,
∴△BFE∽△BCD,
∴一定与△BCD相似的是△BFE,△AFD,△ACE,
故不一定与△BCD相似的是△BAE.
故选D.
∵BD⊥AC,AE⊥BC,
∴∠BDC=∠AEC=90°.
∴∠DBC+∠C=∠EAC+∠C=90°.
∴∠DBC=∠EAC.
∴△ACE∽△BCD.
又
∵∠ADF=∠BDC=90°
∴△AFD∽△BCD.
∵∠FBE=∠DBC、∠BEF=∠BDC=90°,
∴△BFE∽△BCD,
∴一定与△BCD相似的是△BFE,△AFD,△ACE,
故不一定与△BCD相似的是△BAE.
故选D.
3. 如图小明在作业纸上画出(1)、(2)两组三角形,每组各有两个三角形,其边长和角的度数已在图上标注,对于图(1)、(2)中的两个三角形而言,下列说法正确的是( )
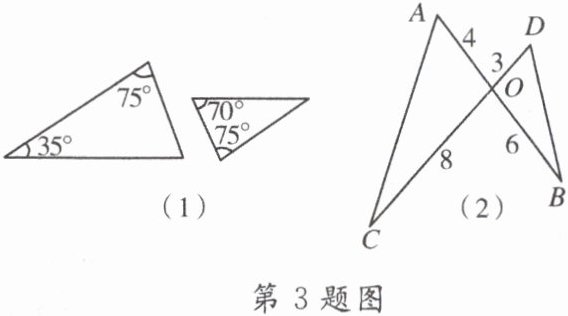
A.都相似
B.都不相似
C.只有①相似
D.只有②相似

A.都相似
B.都不相似
C.只有①相似
D.只有②相似
答案:
3.A [解析]如图①,
∵∠A=35°,∠B=75°,
∴∠C=180°−∠A−∠B=70°.
∵∠E=75°,∠F=70°,
∴∠B=∠E,∠C=∠F.
∴△ABC∽△DEF;

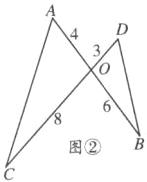
如图②,
∵OA=4,OD=3,OC=8,OB=6,
∴$\frac{OA}{OD}$=$\frac{OC}{OB}$.
∵∠AOC=∠DOB,
∴△AOC∽△DOB.
故选A.
3.A [解析]如图①,
∵∠A=35°,∠B=75°,
∴∠C=180°−∠A−∠B=70°.
∵∠E=75°,∠F=70°,
∴∠B=∠E,∠C=∠F.
∴△ABC∽△DEF;


如图②,
∵OA=4,OD=3,OC=8,OB=6,
∴$\frac{OA}{OD}$=$\frac{OC}{OB}$.
∵∠AOC=∠DOB,
∴△AOC∽△DOB.
故选A.
4. 如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是(
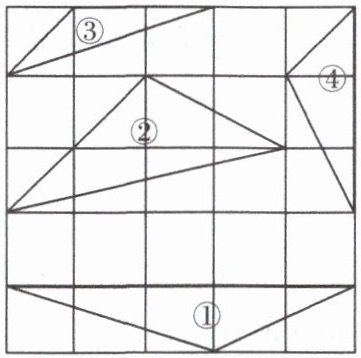
A.①④
B.①③
C.②③
D.②④
B
)
A.①④
B.①③
C.②③
D.②④
答案:
4.B [解析]①号三角形的边长分别为$\sqrt{5}$,$\sqrt{10}$,5;②号三角形的边长分别为$\sqrt{5}$,2$\sqrt{2}$,$\sqrt{17}$;③号三角形的边长分别为$\sqrt{2}$,2,$\sqrt{10}$;④号三角形的边长分别为$\sqrt{2}$,$\sqrt{5}$,3;对应边成比例的是①和③.故选B.
5. 如图所示,在$\triangle ABC中D为AC$边上一点,请你添加一个条件,使$\triangle ABC和\triangle BCD$相似,你所添加的条件是
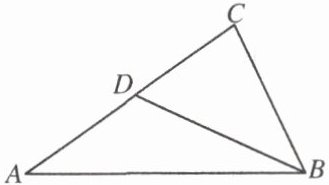
∠A=∠CBD或∠CDB=∠ABC(答案不唯一)
.
答案:
5.∠A=∠CBD或∠CDB=∠ABC(答案不唯一).
6. 为了测量一棵树的高度,小梦在同一时间、同一地点测得小兰身高$1.5m$,她的影子长是$2.4m$,树的影子长是$4m$,则这棵树高有______
2.5
$m$.
答案:
6.2.5 [解析]设树高为h米,
∵同一时刻物高与影长成正比,
∴1.5:2.4=h:4,
解得h=2.5.
∵同一时刻物高与影长成正比,
∴1.5:2.4=h:4,
解得h=2.5.
7. 在平面直角坐标系中有两点$A(4,0)$,$B(0,2)$,如果点$C在x$轴上($C与A$不重合),当点$C$的坐标为
(−1,0)或(1,0)
时,使得$\triangle BOC\backsim\triangle AOB$.
答案:
7.(−1,0)或(1,0) [解析]
∵点A的坐标为(4,0),
∴AO=4,
∵点B的坐标为(0,2),
∴OB=2.
若△BOC∽△AOB,
则$\frac{OC}{OB}$=$\frac{OB}{OA}$,即$\frac{OC}{2}$=$\frac{2}{4}$.
∴OC=1.
故点C的坐标为(−1,0)或(1,0).
∵点A的坐标为(4,0),
∴AO=4,
∵点B的坐标为(0,2),
∴OB=2.
若△BOC∽△AOB,
则$\frac{OC}{OB}$=$\frac{OB}{OA}$,即$\frac{OC}{2}$=$\frac{2}{4}$.
∴OC=1.
故点C的坐标为(−1,0)或(1,0).
8. 如图,已知$\angle 1= \angle 2$,$\angle AED= \angle C$,求证:$\triangle ABC\backsim\triangle ADE$.
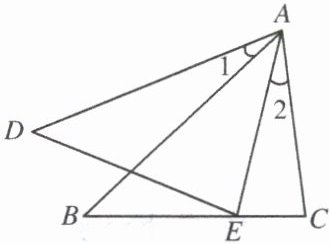
证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
∵∠AED=∠C,
∴△ABC∽△ADE

证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
∵∠AED=∠C,
∴△ABC∽△ADE
答案:
8.证明:
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
∵∠AED=∠C,
∴△ABC∽△ADE;
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
∵∠AED=∠C,
∴△ABC∽△ADE;
9. 如图是一个铁夹子的侧面示意图,点$C$是连接夹面的轴上一点,$CD\perp OA于点D$.这个侧面图是轴对称图形,直线$OC$是它的对称轴.已知$DA = 15mm$,$DO = 24mm$,$DC = 10mm$.求点$A与点B$之间的距离.
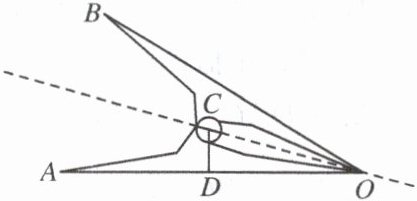

答案:
9.解:如图,连接AB交直线OC于点E,得AB⊥OC,AE=BE,
∴OC=$\sqrt{OD^{2}+CD^{2}}$=$\sqrt{24^{2}+10^{2}}$=26(mm).
∵∠AOE=∠COD,
∠OEA=∠ODC=90°,
∴△OAE∽△OCD.
∴$\frac{AE}{CD}$=$\frac{OA}{OC}$,即$\frac{AE}{10}$=$\frac{39}{26}$,
∴AE=15mm.
∴AB=2AE=30mm.
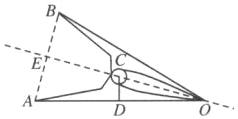
9.解:如图,连接AB交直线OC于点E,得AB⊥OC,AE=BE,
∴OC=$\sqrt{OD^{2}+CD^{2}}$=$\sqrt{24^{2}+10^{2}}$=26(mm).
∵∠AOE=∠COD,
∠OEA=∠ODC=90°,
∴△OAE∽△OCD.
∴$\frac{AE}{CD}$=$\frac{OA}{OC}$,即$\frac{AE}{10}$=$\frac{39}{26}$,
∴AE=15mm.
∴AB=2AE=30mm.

查看更多完整答案,请扫码查看


