2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列各数中,不是无理数的是(
A.$\sqrt{3}$
B.$\sqrt[3]{-27}$
C.$2\pi$
D.$1.343343334…$(小数点后面相邻的两个 4 之间依次多 1 个 3)
B
)A.$\sqrt{3}$
B.$\sqrt[3]{-27}$
C.$2\pi$
D.$1.343343334…$(小数点后面相邻的两个 4 之间依次多 1 个 3)
答案:
B
2. 绝对值是$\sqrt{5}$的实数是(
A.$\pm\sqrt{5}$
B.$\sqrt{5}$
C.$-\sqrt{5}$
D.$\pm5$
A
)A.$\pm\sqrt{5}$
B.$\sqrt{5}$
C.$-\sqrt{5}$
D.$\pm5$
答案:
A
3. 下列说法正确的是(
A.$0.02的平方根是0.2$
B.$\sqrt{18}= 4$
C.$0的立方根是0$
D.$3的立方根是\pm3$
C
)A.$0.02的平方根是0.2$
B.$\sqrt{18}= 4$
C.$0的立方根是0$
D.$3的立方根是\pm3$
答案:
C
4. $\sqrt[3]{-64}$的相反数是(
A.$4$
B.$-4$
C.$\frac{1}{4}$
D.$-\frac{1}{4}$
A
)A.$4$
B.$-4$
C.$\frac{1}{4}$
D.$-\frac{1}{4}$
答案:
A
5. 如图所示,数轴上点$P$所表示的可能是(

A.$\sqrt{6}$
B.$10$
C.$\sqrt{15}$
D.$\sqrt{31}$
C
)
A.$\sqrt{6}$
B.$10$
C.$\sqrt{15}$
D.$\sqrt{31}$
答案:
C
6. 如图,数轴上点$C$所表示的数是(
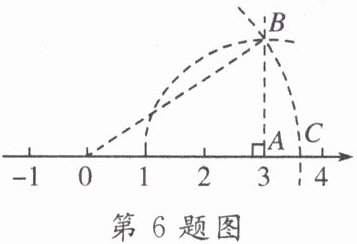
A.$2\sqrt{2}$
B.$3.7$
C.$3.8$
D.$\sqrt{13}$
D
)
A.$2\sqrt{2}$
B.$3.7$
C.$3.8$
D.$\sqrt{13}$
答案:
D
7. 如图所示是一段楼梯,高$BC是3m$,斜边$AC是5m$,如果在楼梯上铺地毯,那么至少需要地毯(
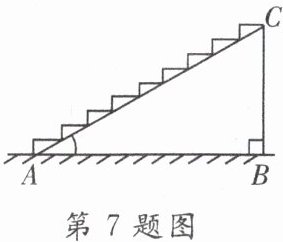
A.$5m$
B.$6m$
C.$7m$
D.$8m$
C
)
A.$5m$
B.$6m$
C.$7m$
D.$8m$
答案:
C
8. 勾股定理是人类最伟大的科学发现之一,在我国古代《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内.若图中阴影部分图形的面积为$3$,则较小两个正方形重叠部分图形的面积为(
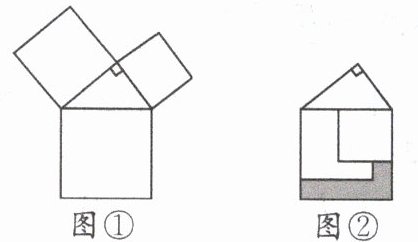
A.$2$
B.$3$
C.$5$
D.$6$
B
)
A.$2$
B.$3$
C.$5$
D.$6$
答案:
B [解析]设直角三角形的斜边长为 $ c $,较长直角边为 $ b $,较短直角边为 $ a $,由勾股定理,得 $ c^{2}=a^{2}+b^{2} $,阴影部分的面积 $ =c^{2}-b^{2}-a(c-b)=a^{2}-ac+ab=a(a+b-c)=3 $,较小两个正方形重叠部分的宽 $ =a-(c-b) $,长 $ =a $,则较小两个正方形重叠部分的面积 $ =a(a+b-c)=3 $,故选 B.
9. 化简$|\sqrt{2}-3|+\sqrt{18}$的结果是
$ 3+2\sqrt{2} $
.
答案:
$ 3+2\sqrt{2} $
10. 已知$\sqrt{102.01}= 10.1$,则$\sqrt{1.0201}= $
1.01
.
答案:
1.01
11. 对于任意两个实数$a$、$b$,定义运算“☆”为$a☆b= \sqrt{a+b}$.如$3☆2= \sqrt{3+2}= \sqrt{5}$,根据定义可得$4☆8= $
$2\sqrt{3}$
.
答案:
$ 2\sqrt{3} $
12. 设$x\lt y\lt0$,则$\sqrt{x^{2}+1}$
>
$\sqrt{y^{2}+1}$.(填“$>$”,“$<$”或“$=$”)
答案:
$ > $
13. 实数$a$、$b$在数轴上所对应的点如图所示,则$|\sqrt{3}-b|+|a+\sqrt{3}|+\sqrt{a^{2}}$的值
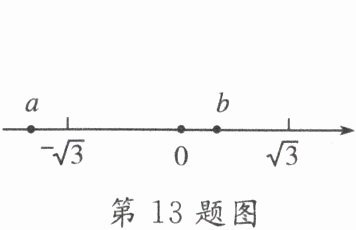
$-2a - b$
.
答案:
$ -2a - b $ [解析]由数轴可得 $ a<-\sqrt{3},0<b<\sqrt{3} $,故 $ |\sqrt{3}-b|+|a+\sqrt{3}|+\sqrt{a^{2}} $ $ =\sqrt{3}-b-(a+\sqrt{3})-a $ $ =\sqrt{3}-b-a-\sqrt{3}-a $ $ =-2a - b $.
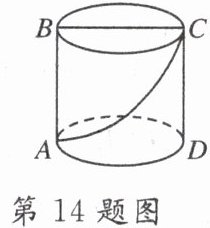
14. 如图,一圆柱体的底面周长为$24cm$,高$AB为9cm$,$BC$是上底面的直径.一只蚂蚁从点$A$出发,沿着圆柱的侧面爬行到点$C$,则蚂蚁爬行的最短路程是______$cm$.

答案:
15 [解析]如图所示.

由于圆柱体的底面周长为 $ 24 \, \text{cm} $,则 $ AD = 24 × \frac{1}{2} = 12 \, \text{cm} $. 又 $ \because CD = AB = 9 \, \text{cm} $,$ \therefore AC = \sqrt{12^{2}+9^{2}} = 15 \, \text{cm} $. 故蚂蚁从点 $ A $ 出发,沿着圆柱体的侧面爬行到点 $ C $ 的最短路程是 $ 15 \, \text{cm} $.
15 [解析]如图所示.

由于圆柱体的底面周长为 $ 24 \, \text{cm} $,则 $ AD = 24 × \frac{1}{2} = 12 \, \text{cm} $. 又 $ \because CD = AB = 9 \, \text{cm} $,$ \therefore AC = \sqrt{12^{2}+9^{2}} = 15 \, \text{cm} $. 故蚂蚁从点 $ A $ 出发,沿着圆柱体的侧面爬行到点 $ C $ 的最短路程是 $ 15 \, \text{cm} $.
15. (8 分)计算:
(1)$\sqrt{16}-(\sqrt[3]{-8}+4)$;
(2)$(-1)^{2022}+(-9)×|-\frac{2}{9}|-4^{2}÷(-2)$;
(3)$(-3)^{2}+\sqrt[3]{-8}+|1-\sqrt{2}|$;
(4)$4×(\sqrt{3}+\sqrt{7})^{0}+\sqrt[3]{27}×\sqrt{8}+|1+\sqrt{2}|$;
(1)$\sqrt{16}-(\sqrt[3]{-8}+4)$;
(2)$(-1)^{2022}+(-9)×|-\frac{2}{9}|-4^{2}÷(-2)$;
(3)$(-3)^{2}+\sqrt[3]{-8}+|1-\sqrt{2}|$;
(4)$4×(\sqrt{3}+\sqrt{7})^{0}+\sqrt[3]{27}×\sqrt{8}+|1+\sqrt{2}|$;
答案:
(1)解:原式$=4 - (-2 + 4)$
$=4 - 2$
$=2$
(2)解:原式$=1 + (-9)×\frac{2}{9} - 16÷(-2)$
$=1 - 2 + 8$
$=7$
(3)解:原式$=9 + (-2) + (\sqrt{2} - 1)$
$=9 - 2 + \sqrt{2} - 1$
$=\sqrt{2} + 6$
(4)解:原式$=4×1 + 3×2\sqrt{2} + (1 + \sqrt{2})$
$=4 + 6\sqrt{2} + 1 + \sqrt{2}$
$=7\sqrt{2} + 5$
(1)解:原式$=4 - (-2 + 4)$
$=4 - 2$
$=2$
(2)解:原式$=1 + (-9)×\frac{2}{9} - 16÷(-2)$
$=1 - 2 + 8$
$=7$
(3)解:原式$=9 + (-2) + (\sqrt{2} - 1)$
$=9 - 2 + \sqrt{2} - 1$
$=\sqrt{2} + 6$
(4)解:原式$=4×1 + 3×2\sqrt{2} + (1 + \sqrt{2})$
$=4 + 6\sqrt{2} + 1 + \sqrt{2}$
$=7\sqrt{2} + 5$
查看更多完整答案,请扫码查看


