《2025年鲁人泰斗假期好时光八年级数学青岛版》

24. (8分)某水果店$11$月份购进甲、乙两种水果共花费$1700$元,其中甲种水果$8$元/千克,乙种水果$18$元/千克.$12$月份,这两种水果的进价上调为甲种水果$10$元/千克,乙种水果$20$元/千克.
(1)若该店$12月份购进这两种水果的数量与11$月份都相同,将多支付货款$300$元,求该店$11$月份购进甲、乙两种水果分别是多少千克？
(2)若$12月份将这两种水果进货总量减少到120$千克,设购进甲种水果$a$千克,需要支付的货款为$w$元,求$w与a$的函数表达式；
(3)在(2)的条件下,若甲种水果不超过$90$千克,则$12$月份该店需要支付这两种水果的货款最少应是多少元？

答案： 24. 解：
(1)设该店11月份购进甲种水果$x$千克，购进乙种水果$y$千克，根据题意，得
$\begin{cases}8x + 18y = 1700 \\10x + 20y = 1700 + 300\end{cases}$
解得$\begin{cases}x = 100 \\y = 50\end{cases}$
答：该店11月份购进甲种水果100千克，购进乙种水果50千克。
(2)设购进甲种水果$a$千克，需要支付的货款为$w$元，则购进乙种水果$(120 - a)$千克，根据题意，得
$w = 10a + 20(120 - a) = -10a + 2400$
(3)根据题意，得$a \leq 90$，由
(2)得$w = -10a + 2400$
$\because -10 \lt 0$，$w$随$a$的增大而减小
$\therefore$当$a = 90$时，$w$有最小值，$w_{\text{最小}} = -10×90 + 2400 = 1500$（元）
答：12月份该店需要支付这两种水果的货款最少应是1500元。

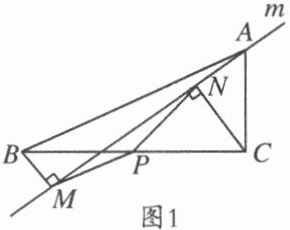
25. (10分)如图$1$,在$\triangle ABC$中,点$P为BC$边中点,直线$m绕顶点A$旋转,$BM⊥直线m于点M$,$CN⊥直线m于点N$,连接$PM$、$PN$.在直线$m绕点A$旋转的过程中,
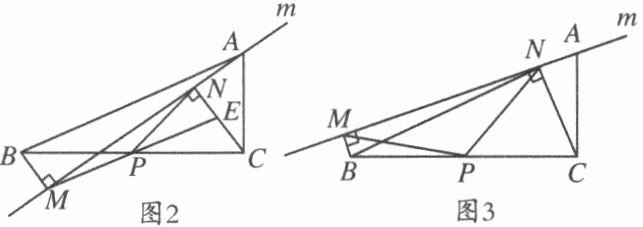
(1)如图$2$,当点$B$,$P在直线m$的异侧时,延长$MP交CN于点E$,
①求证：$\triangle BPM≌\triangle CPE$；
②求证：$PM= PN$；
(2)如图$3$,当点$B$,$P在直线m$的同侧时,其它条件不变,
①$PM= PN$还成立吗？若成立,请给予证明；若不成立,请说明理由；
②当$∠NMP= 30^{\circ}$时,请直接写出$BM$、$CN$、$PM$之间的关系.

答案：
25. 解:
(1) 证明: ①$\because BM\perp$直线$m$于点$M$,$CN\perp$直线$m$于点$N$, $\therefore\angle BMN=\angle CNM = 90^{\circ}$. $\therefore BM// CN$. $\therefore\angle MBP=\angle ECP$. 又$\because$点$P$为$BC$边中点, $\therefore BP = CP$. 在$\triangle BPM$和$\triangle CPE$中, $\begin{cases}\angle MBP=\angle ECP\\BP = CP\\\angle BPM=\angle CPE\end{cases}$, $\therefore\triangle BPM\cong\triangle CPE(ASA)$. ②$\because\triangle BPM\cong\triangle CPE$, $\therefore PM = PE$. $\therefore PM=\frac{1}{2}ME$. $\therefore$在$Rt\triangle MNE$中,$PN=\frac{1}{2}ME$. $\therefore PM = PN$.
(2) ①成立,如图,延长$MP$与$NC$的延长线相交于点$E$,

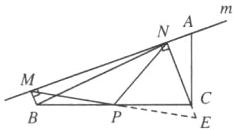
$\because BM\perp$直线$m$于点$M$,$CN\perp$直线$m$于点$N$, $\therefore\angle BMN=\angle CNM = 90^{\circ}$. $\therefore\angle BMN+\angle CNM = 180^{\circ}$. $\therefore BM// CN$. $\therefore\angle MBP=\angle ECP$. 又$\because P$为$BC$中点,
$\therefore BP = CP$. 在$\triangle BPM$和$\triangle CPE$中, $\begin{cases}\angle MBP=\angle ECP\\BP = CP\\\angle BPM=\angle CPE\end{cases}$, $\therefore\triangle BPM\cong\triangle CPE(ASA)$. $\therefore PM = PE$. $\therefore PM=\frac{1}{2}ME$. 则$Rt\triangle MNE$中,$PN=\frac{1}{2}ME$, $\therefore PM = PN$.
②$PM = CN + BM$, 理由: $\because BM\perp m$, $\therefore\angle BMN = 90^{\circ}$. $\because\angle NMP = 30^{\circ}$, $\therefore\angle PMB = 90^{\circ}-\angle PMN = 60^{\circ}$. 由①知,$\triangle BPM\cong\triangle CPE$, $\therefore BM = CE,PM = PE,\angle E=\angle BMP = 60^{\circ}$. $\therefore\triangle PEN$是等边三角形. $\therefore PM = NE = CN + CE = CN + BM$.