2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 如图,四边形 ABCD 与四边形$A'B'C'D'$位似,点 O 为位似中心,若$OB:OB' = 2:3$,则四边形 ABCD 与四边形$A'B'C'D'$的面积比为(
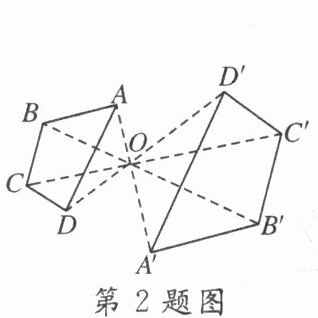
A.$2:3$
B.$2:5$
C.$4:9$
D.$4:25$
C
)
A.$2:3$
B.$2:5$
C.$4:9$
D.$4:25$
答案:
C [解析]
∵四边形 $ABCD$ 与四边形 $A'B'C'D'$ 位似,
∴四边形 $ABCD \backsim$ 四边形 $A'B'C'D'$, $AB // A'B'$.
∴$\triangle OAB \backsim \triangle OA'B'$.
同理 $\triangle OBC \backsim \triangle OB'C'$, $\triangle OCD \backsim \triangle OC'D'$.
∴$\frac{AB}{A'B'} = \frac{OB}{OB'} = \frac{2}{3}$.
∴四边形 $ABCD$ 与四边形 $A'B'C'D'$ 的面积比 $= (\frac{AB}{A'B'})^2 = \frac{4}{9}$. 故选C.
∵四边形 $ABCD$ 与四边形 $A'B'C'D'$ 位似,
∴四边形 $ABCD \backsim$ 四边形 $A'B'C'D'$, $AB // A'B'$.
∴$\triangle OAB \backsim \triangle OA'B'$.
同理 $\triangle OBC \backsim \triangle OB'C'$, $\triangle OCD \backsim \triangle OC'D'$.
∴$\frac{AB}{A'B'} = \frac{OB}{OB'} = \frac{2}{3}$.
∴四边形 $ABCD$ 与四边形 $A'B'C'D'$ 的面积比 $= (\frac{AB}{A'B'})^2 = \frac{4}{9}$. 故选C.
3. 已知$\triangle ABC和\triangle A'B'C'$是位似图形,$\triangle A'B'C'$的面积6cm²,周长是$\triangle ABC$的一半,$AB = 8cm$,则 AB 边上的高等于(
A.$3cm$
B.$6cm$
C.$9cm$
D.$12cm$
6cm
)A.$3cm$
B.$6cm$
C.$9cm$
D.$12cm$
答案:
B [解析]由题意知 $\triangle ABC \backsim \triangle A'B'C'$, $\triangle A'B'C'$ 的周长是 $\triangle ABC$ 的一半,
∴$\triangle ABC$ 与 $\triangle A'B'C'$ 的相似比为 $2:1$.
∴$S_{\triangle ABC} = 4S_{\triangle A'B'C'} = 24\ \text{cm}^2$.
∴$AB$ 边上的高等于 $6\ \text{cm}$. 故选B.
∴$\triangle ABC$ 与 $\triangle A'B'C'$ 的相似比为 $2:1$.
∴$S_{\triangle ABC} = 4S_{\triangle A'B'C'} = 24\ \text{cm}^2$.
∴$AB$ 边上的高等于 $6\ \text{cm}$. 故选B.
4. 如图,$\triangle ABC$的两个顶点 B,C 均在第一象限,以点$A(0,1)$为位似中心,在 y 轴左侧作$\triangle ABC的位似图形\triangle ADE$,$\triangle ABC与\triangle ADE的相似比为1:2$,若点 C 的纵坐标是 m,则其对应点 E 的纵坐标是(
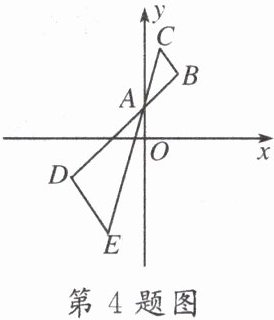
A.$\frac{-m + 3}{2}$
B.$2m + 3$
C.$-(2m + 3)$
D.$-2m + 3$
D
)
A.$\frac{-m + 3}{2}$
B.$2m + 3$
C.$-(2m + 3)$
D.$-2m + 3$
答案:
D [解析]设点 $C$ 的纵坐标为 $m$, 则 $A$, $C$ 间的纵坐标的长度为 $(m - 1)$,
∵$\triangle ABC$ 放大到原来的 $2$ 倍得到 $\triangle ADE$,
∴$E$, $A$ 间的纵坐标的长度为 $2(m - 1)$.
∴点 $E$ 的纵坐标是 $-[2(m - 1) - 1] = -(2m - 3) = -2m + 3$.
故选D.
∵$\triangle ABC$ 放大到原来的 $2$ 倍得到 $\triangle ADE$,
∴$E$, $A$ 间的纵坐标的长度为 $2(m - 1)$.
∴点 $E$ 的纵坐标是 $-[2(m - 1) - 1] = -(2m - 3) = -2m + 3$.
故选D.
5. 在平面直角坐标系中,已知点$A(-4,2)$,$B(-6,-4)$,以原点 O 为位似中心,相似比为$\frac{1}{2}$,把$\triangle ABO$缩小,则点 A 的对应点$A'$的坐标是(
A.$(-2,1)$
B.$(-8,4)$
C.$(-8,4)或(8,-4)$
D.$(-2,1)或(2,-1)$
D
)A.$(-2,1)$
B.$(-8,4)$
C.$(-8,4)或(8,-4)$
D.$(-2,1)或(2,-1)$
答案:
D [解析]
∵点 $A(-4,2)$, 以原点 $O$ 为位似中心, 相似比为 $\frac{1}{2}$,
∴点 $A$ 的对应点 $A'$ 的坐标是 $(-4 × \frac{1}{2}, 2 × \frac{1}{2})$ 或 $(-4 × (-\frac{1}{2}), 2 × (-\frac{1}{2}))$,
即 $(-2,1)$ 或 $(2,-1)$.
故选D.
∵点 $A(-4,2)$, 以原点 $O$ 为位似中心, 相似比为 $\frac{1}{2}$,
∴点 $A$ 的对应点 $A'$ 的坐标是 $(-4 × \frac{1}{2}, 2 × \frac{1}{2})$ 或 $(-4 × (-\frac{1}{2}), 2 × (-\frac{1}{2}))$,
即 $(-2,1)$ 或 $(2,-1)$.
故选D.
6. 如图,$\triangle DEF与\triangle ABC$位似,点 O 为位似中心,已知$OF:OC = 1:2$,则$\triangle DEF与\triangle ABC$的周长之比是
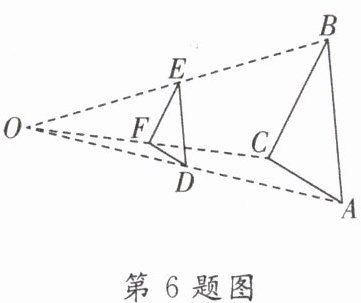
$1:2$
。
答案:
$1:2$
7. 如图,四边形 ABCD 与四边形 EFGH 位似,位似中心点是点 O,$\frac{OE}{OA}= \frac{3}{5}$,则$\frac{FG}{BC}=$
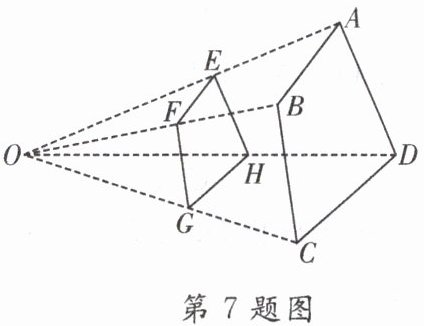
$\frac{3}{5}$
。
答案:
$\frac{3}{5}$ [解析]
∵四边形 $ABCD$ 与四边形 $EFGH$ 位似,
∴$\triangle OEF \backsim \triangle OAB$, $\triangle OFG \backsim \triangle OBC$.
∴$\frac{OE}{OA} = \frac{OF}{OB} = \frac{3}{5}$.
∴$\frac{FG}{BC} = \frac{OF}{OB} = \frac{3}{5}$.
∵四边形 $ABCD$ 与四边形 $EFGH$ 位似,
∴$\triangle OEF \backsim \triangle OAB$, $\triangle OFG \backsim \triangle OBC$.
∴$\frac{OE}{OA} = \frac{OF}{OB} = \frac{3}{5}$.
∴$\frac{FG}{BC} = \frac{OF}{OB} = \frac{3}{5}$.
8. 如图,点$E(-6,2)$,$F(-2,-2)$,以原点 O 为位似中心,相似比为$1:2$,把$\triangle EFO$在 y 轴右侧缩小,则点 E 的对应点$E_1$的坐标为
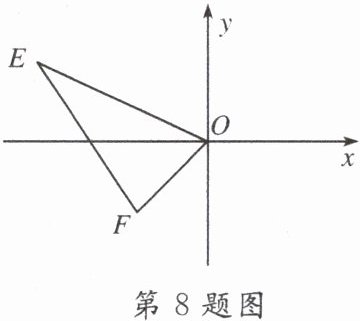
$(3,-1)$
。
答案:
$(3,-1)$ [解析]
∵以原点 $O$ 为位似中心, 相似比为 $1:2$, 把 $\triangle EFO$ 在 $y$ 轴右侧缩小, $E(-6,2)$,
∴点 $E$ 的对应点 $E_1$ 的坐标为 $(6 × \frac{1}{2}, -2 × \frac{1}{2})$, 即 $(3,-1)$.
∵以原点 $O$ 为位似中心, 相似比为 $1:2$, 把 $\triangle EFO$ 在 $y$ 轴右侧缩小, $E(-6,2)$,
∴点 $E$ 的对应点 $E_1$ 的坐标为 $(6 × \frac{1}{2}, -2 × \frac{1}{2})$, 即 $(3,-1)$.
9. 在平面直角坐标系中,已知$A(-3,3)$,$B(-6,0)$,以原点 O 为位似中心,将线段 AB 放大为原来的 2 倍,得到线段$A'B'$,则$A'B'$的中点坐标是
$(-9,3)$ 或 $(9,-3)$
。
答案:
$(-9,3)$ 或 $(9,-3)$ [解析]
∵点 $A$ 的坐标为 $(-3,3)$, 点 $B$ 的坐标为 $(-6,0)$,
∴$AB$ 的中点坐标为 $(-\frac{9}{2}, \frac{3}{2})$.
∵以原点 $O$ 为位似中心, 将线段 $AB$ 放大为原来的 $2$ 倍, 得到线段 $A'B'$,
∴$A'B'$ 的中点坐标为 $(-\frac{9}{2} × 2, \frac{3}{2} × 2)$ 或 $(\frac{9}{2} × 2, -\frac{3}{2} × 2)$,
即 $(-9,3)$ 或 $(9,-3)$.
∵点 $A$ 的坐标为 $(-3,3)$, 点 $B$ 的坐标为 $(-6,0)$,
∴$AB$ 的中点坐标为 $(-\frac{9}{2}, \frac{3}{2})$.
∵以原点 $O$ 为位似中心, 将线段 $AB$ 放大为原来的 $2$ 倍, 得到线段 $A'B'$,
∴$A'B'$ 的中点坐标为 $(-\frac{9}{2} × 2, \frac{3}{2} × 2)$ 或 $(\frac{9}{2} × 2, -\frac{3}{2} × 2)$,
即 $(-9,3)$ 或 $(9,-3)$.
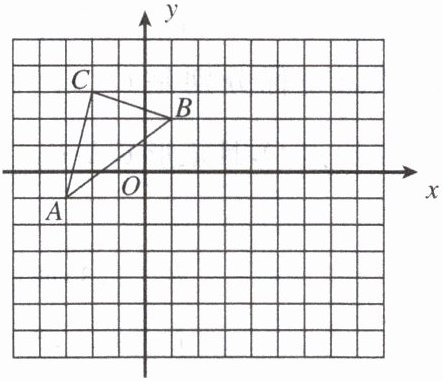
10. 如图,在平面直角坐标系中,$\triangle ABC$的顶点 A 的坐标为$(-3,-1)$,顶点 B,C 都在小正方形的格点上。
(1)点 B 的坐标为____,点 C 的坐标为____;
(2)以原点 O 为位似中心,在所给的网格中画出一个$\triangle A_1B_1C_1$,使得$\triangle A_1B_1C_1与\triangle ABC$位似,且相似比为$2:1$。
(1)点 B 的坐标为____,点 C 的坐标为____;
(2)以原点 O 为位似中心,在所给的网格中画出一个$\triangle A_1B_1C_1$,使得$\triangle A_1B_1C_1与\triangle ABC$位似,且相似比为$2:1$。

答案:
(1) $(1,2)$ $(-2,3)$
(2) 如图, $\triangle A_1B_1C_1$ 即为所求作.

(1) $(1,2)$ $(-2,3)$
(2) 如图, $\triangle A_1B_1C_1$ 即为所求作.

查看更多完整答案,请扫码查看


