《2025年鲁人泰斗假期好时光八年级数学青岛版》

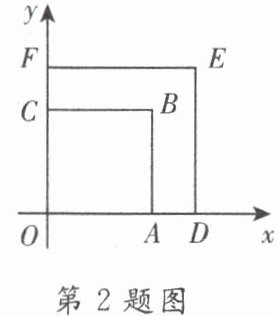
1. 如图,矩形 EFGO 的两边在坐标轴上,点 O 为平面直角坐标系的原点,以 y 轴上的某一点为位似中心,作位似图形 ABCD,且点 B,F 的坐标分别为$(-4,4)$,$(2,1)$,则位似中心的坐标为( )


A.$(0,3)$
B.$(0,2.5)$
C.$(0,2)$
D.$(0,1.5)$

答案：
C [解析]如图, 连接 $BF$ 交 $y$ 轴于点 $P$,

∵四边形 $ABCD$ 和四边形 $EFGO$ 是矩形, 点 $B$, $F$ 的坐标分别为 $(-4,4)$, $(2,1)$,
∴点 $C$ 的坐标为 $(0,4)$, 点 $G$ 的坐标为 $(0,1)$.
∴$CG = 3$.
∵$BC // GF$,
∴$\frac{GP}{PC} = \frac{GF}{BC} = \frac{1}{2}$.
∴$GP = 1$, $PC = 2$.
∴点 $P$ 的坐标为 $(0,2)$. 故选C.

2. 如图,正方形 OABC 与正方形 ODEF 是位似图形,O 为位似中心,相似比为$1:\sqrt{2}$,点 A 的坐标为$(1,0)$,则点 E 的坐标为(C)

A.$(\sqrt{2},0)$
B.$(\frac{3}{2},\frac{3}{2})$
C.$(\sqrt{2},\sqrt{2})$
D.$(2,2)$

答案： C [解析]
∵正方形 $OABC$ 与正方形 $ODEF$ 是位似图形, $O$ 为位似中心, 相似比为 $1:\sqrt{2}$,
∴$OA:OD = 1:\sqrt{2}$.
∵点 $A$ 的坐标为 $(1,0)$, 即 $OA = 1$,
∴$OD = \sqrt{2}$.
∵四边形 $ODEF$ 是正方形,
∴$DE = OD = \sqrt{2}$.
∴点 $E$ 的坐标为 $(\sqrt{2},\sqrt{2})$. 故选C.

3. 如图,$\triangle ABC$在正方形格纸中,
(1)请在正方形格纸上建立平面直角坐标系,使$A(2,3)$,$C(6,2)$,并写出点 B 的坐标；
(2)以坐标原点 O 为位似中心,相似比为$2:1$,在第一象限内将$\triangle ABC$放大,画出放大后的图形$\triangle A_1B_1C_1$,并写出点 A 的对应点$A_1$的坐标；
(3)若线段 AB 绕原点 O 旋转$90^{\circ}$后点 B 的对应点为$B_2$,写出点$B_2$的坐标。

答案：
解:
(1) 建立平面直角坐标系, 如图所示,
由图形可得 $B(2,1)$.
(2) 如图所示, $\triangle A_1B_1C_1$ 即为所求, 由图形可得 $A_1(4,6)$.
(3) 线段 $AB$ 绕原点 $O$ 顺时针 (或逆时针) 旋转 $90^{\circ}$ 后点 $B$ 的对应点 $B_2$ 的坐标为 $(1,-2)$ 或 $(-1,2)$.

1. 如图所示,$\triangle DEF是\triangle ABC$位似图形的几种画法,其中正确的个数是(A)

A.4
B.3
C.2
D.1

答案： A