《2025年鲁人泰斗假期好时光八年级数学青岛版》

17. (10分)为了测量路灯($OS$)的高度,把一根长 $1.5$ 米的竹竿($AB$)竖直立在水平地面上,测得竹竿的影子($BC$)长为 $1$ 米,然后拿竹竿向远离路灯方向走了 $4$ 米($BB'$),再把竹竿竖立在地面上,测得竹竿的影子($B'C'$)长为 $1.8$ 米,求路灯离地面的高度.

解：$\because AB⊥OC',OS⊥OC'$，
$\therefore AB// OS$．
$\therefore \triangle ABC\backsim \triangle SOC$．
$\therefore \frac {BC}{BC+OB}=\frac {AB}{OS}$，即$\frac {1}{1+OB}=\frac {1.5}{h}$．
解得$OB=\frac {2}{3}h - 1$，①
同理，$\because A'B'⊥OC'$，
$\therefore \triangle A'B'C'\backsim \triangle SOC'$．
$\therefore \frac {B'C'}{B'C'+BB'+OB}=\frac {A'B'}{OS}$，$\frac {1.8}{1.8 + 4 + OB}=\frac {1.5}{h}$．②
把①代入②，得$\frac {1.8}{5.8+\frac {2}{3}h - 1}=\frac {1.5}{h}$，
解得$h=$9．
答：路灯离地面的高度是9米．

答案： 解：$\because AB⊥OC',OS⊥OC'$，
$\therefore AB// OS$．
$\therefore \triangle ABC\backsim \triangle SOC$．
$\therefore \frac {BC}{BC+OB}=\frac {AB}{OS}$，即$\frac {1}{1+OB}=\frac {1.5}{h}$．
解得$OB=\frac {2}{3}h - 1$，①
同理，$\because A'B'⊥OC'$，
$\therefore \triangle A'B'C'\backsim \triangle SOC'$．
$\therefore \frac {B'C'}{B'C'+BB'+OB}=\frac {A'B'}{OS}$，$\frac {1.8}{1.8 + 4 + OB}=\frac {1.5}{h}$．②
把①代入②，得$\frac {1.8}{5.8+\frac {2}{3}h - 1}=\frac {1.5}{h}$，
解得$h=9$．
答：路灯离地面的高度是$9$米．

18. (10分)如图,$AC$ 为 $□ ABCD$ 的对角线,作 $\angle ABE = \angle ACB$,$BE$ 交边 $AD$ 于点 $E$,交 $AC$ 于点 $F$.
(1)求证：$AE^2 = EF \cdot BE$；
(2)若 $EF = 1$,$E$ 是 $AD$ 的中点,求边 $BC$ 的长.

(1)证明：$\because$ 四边形$ABCD$为平行四边形，
$\therefore AD// BC$．
$\therefore ∠DAC=∠ACB$．
$\because ∠ACB=∠ABE$，
$\therefore ∠EAF=∠EBA$．
$\because ∠AEF=∠BEA$，
$\therefore \triangle EAF\backsim \triangle EBA$．
$\therefore EA:EB=EF:EA$．
$\therefore AE^{2}=EF\cdot BE$；
(2) $\because$ 四边形$ABCD$为平行四边形，
$\therefore AD=BC$．
$\because E$是边$AD$的中点，
$\therefore BC=2AE$．
$\because AE// BC$，
$\therefore \triangle EAF\backsim \triangle BCF$．
$\therefore \frac {AE}{CB}=\frac {EF}{BF}=\frac {1}{2}$．
$\therefore BF=2EF=2$．
$\therefore BE=3$．
$\because AE^{2}=EF\cdot BE=1×3=3$，
$\therefore AE=\sqrt {3}$．
$\therefore BC=2AE=$$2\sqrt{3}$．

答案： 解：（1）证明：$\because$ 四边形$ABCD$为平行四边形，
$\therefore AD// BC$．
$\therefore ∠DAC=∠ACB$．
$\because ∠ACB=∠ABE$，
$\therefore ∠EAF=∠EBA$．
$\because ∠AEF=∠BEA$，
$\therefore \triangle EAF\backsim \triangle EBA$．
$\therefore EA:EB=EF:EA$．
$\therefore AE^{2}=EF\cdot BE$；
（2）$\because$ 四边形$ABCD$为平行四边形，
$\therefore AD=BC$．
$\because E$是边$AD$的中点，
$\therefore BC=2AE$．
$\because AE// BC$，
$\therefore \triangle EAF\backsim \triangle BCF$．
$\therefore \frac {AE}{CB}=\frac {EF}{BF}=\frac {1}{2}$．
$\therefore BF=2EF=2$．
$\therefore BE=3$．
$\because AE^{2}=EF\cdot BE=1×3=3$，
$\therefore AE=\sqrt {3}$．
$\therefore BC=2AE=2\sqrt {3}$．

19. (10分)如图,在正方形 $ABCD$ 中,在 $BC$ 边上取中点 $E$,连接 $ED$,过点 $E$ 作 $EF \perp ED$ 交 $AB$ 于点 $G$,交 $DA$ 的延长线于点 $F$.
(1)求证：$\triangle ECD \sim \triangle DEF$；
证明：$\because$ 四边形$ABCD$是正方形，$EF⊥ED$，
$\therefore ∠FED=∠C=90^{\circ },BC// AD$．
$\therefore ∠CED=∠FDE$．
$\therefore \triangle ECD\backsim \triangle DEF$．
(2)若 $CD = 4$,求 $AF$ 的长.
解：$\because$ 四边形$ABCD$是正方形，
$\therefore ∠C=90^{\circ },AD=BC=CD=4$．
$\because E$为$BC$的中点，
$\therefore CE=\frac {1}{2}BC=2$．
在$Rt\triangle DCE$中，由勾股定理，得$ED=\sqrt {CE^{2}+DC^{2}}=\sqrt {2^{2}+4^{2}}=2\sqrt {5}$，
$\because \triangle ECD\backsim \triangle DEF$，
$\therefore \frac {CE}{ED}=\frac {ED}{DF}$．
$\therefore \frac {2}{2\sqrt {5}}=\frac {2\sqrt {5}}{DF}$．
解得$DF=10$，
$\because AD=4$，
$\therefore AF=DF - AD=10 - 4=$6．

答案： 解：（1）证明：$\because$ 四边形$ABCD$是正方形，$EF⊥ED$，
$\therefore ∠FED=∠C=90^{\circ },BC// AD$．
$\therefore ∠CED=∠FDE$．
$\therefore \triangle ECD\backsim \triangle DEF$．
（2）$\because$ 四边形$ABCD$是正方形，
$\therefore ∠C=90^{\circ },AD=BC=CD=4$．
$\because E$为$BC$的中点，
$\therefore CE=\frac {1}{2}BC=2$．
在$Rt\triangle DCE$中，由勾股定理，得$ED=\sqrt {CE^{2}+DC^{2}}=\sqrt {2^{2}+4^{2}}=2\sqrt {5}$，
$\because \triangle ECD\backsim \triangle DEF$，
$\therefore \frac {CE}{ED}=\frac {ED}{DF}$．
$\therefore \frac {2}{2\sqrt {5}}=\frac {2\sqrt {5}}{DF}$．
解得$DF=10$，
$\because AD=4$，
$\therefore AF=DF - AD=10 - 4=6$．

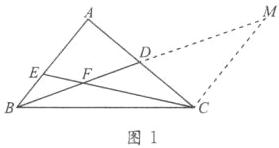
20. (12分)如图,在 $\triangle ABC$ 中,$BD$ 是中线,点 $E$ 是 $AB$ 上一点,$CE$ 与 $BD$ 交于点 $F$,$EB = EF$.
(1)在图1中找出与线段 $AB$ 相等的线段,并证明；
(2)在图2中,若 $\angle ADB = 90^{\circ} - \frac{1}{2}\angle ABD$,$\frac{AB}{AC} = k$,求 $\frac{DF}{BF}$ 的值(用含 $k$ 的代数式表示).

答案：
解：（1）$CF=AB$．理由如下：
如图$1$，延长$BD$至点$M$，使$MD=BD$．
$\because D$是$AC$的中点，

$\therefore AD=CD$．
在$\triangle ADB$与$\triangle CDM$中，
$\left\{\begin{array}{l} AD=CD,\\ ∠ADB=∠CDM,\\ BD=MD,\end{array}\right.$
$\therefore \triangle ADB\cong \triangle CDM(SAS)$．
$\therefore AB=CM,∠ABD=∠CMD$．
$\because EB=EF$，
$\therefore ∠ABD=∠EFB$．
$\because ∠EFB=∠CFM$，
$\therefore ∠CFM=∠CMD$．
$\therefore CM=CF$．
$\because AB=CM$，
$\therefore CF=AB$．
（2）$\because ∠ADB=90^{\circ }-\frac {1}{2}∠ABD$，
设$∠ABD=\alpha$，则$∠ADB=90^{\circ }-\frac {1}{2}\alpha$．
$\therefore ∠BAD=180^{\circ }-∠ABD-∠ADB=180^{\circ }-\alpha -(90^{\circ }-\frac {1}{2}\alpha)=90^{\circ }-\frac {1}{2}\alpha$．
$\therefore ∠ADB=∠BAD$．
$\therefore BD=BA$．
如图$2$，在$FD$的延长线上取点$M$，使$FM=FC$，连接$CM$．

$\because ∠DFC=∠ABD,BD=BA,FM=FC$，
$\therefore ∠M=∠BAD=∠ADB=∠CDM$．
$\therefore MC=CD=AD$．
设$MC=CD=AD=a$，
由（1）知$CF=AB$，
$\therefore FM=BD$．
$\therefore DM=BF$．
$\because AB=kAC$，
$\therefore FM=CF=BD=AB=2ka$．
$\because ∠ADB=∠M,∠BAD=∠CDM$，
$\therefore \triangle ABD\backsim \triangle DCM$．
$\therefore \frac {AD}{DM}=\frac {AB}{DC}=2k$．
$\therefore \frac {a}{DM}=2k$．
$\therefore BF=DM=\frac {a}{2k}$．
$\therefore FD=BD - BF=2ka-\frac {a}{2k}=\frac {4k^{2}-1}{2k}a$．
$\therefore \frac {DF}{BF}=\frac {\frac {4ak^{2}-a}{2k}}{\frac {a}{2k}}=\frac {4ak^{2}-a}{a}=4k^{2}-1$．