《2025年鲁人泰斗假期好时光八年级数学青岛版》

1. 已知$a ＜ b$,则下列四个不等式中,不正确的是(B)
A.$a - 2 ＜ b - 2$
B.$-2a ＜ -2b$
C.$2a ＜ 2b$
D.$a + 2 ＜ b + 2$

答案： B

2. 如果$a ＜ b$,$c ＜ 0$,那么下列不等式中成立的是(D)
A.$a + c ＞ b + c$
B.$ac ＜ bc$
C.$ac^{2} ＞ bc^{2}$
D.$ac + 1 ＞ bc + 1$

答案： D

3. 不等式$x(x + 2) - 4 ＞ x^{2}$的解集为(C)
A.$x ＞ 4$
B.$x ＞ -2$
C.$x ＞ 2$
D.$x ＜ 2$

答案： C

4. 解不等式$\frac{1 + x}{2} - \frac{2x + 1}{3} \leq 1$,并把解集表示在数轴上。

答案：
解:两边同时乘6,得$3(1+x)-2(2x+1)\leq6$，
　去括号,得$3+3x-4x-2\leq6$，
　移项、合并同类项,得$-x\leq5$，
　解得$x\geq-5$。
　表示在数轴上为

5. 已知不等式$x + 8 ＞ 4x + m$($m$是常数)的解集是$x ＜ 3$,求$m$的值。

答案： 解:解不等式$x+8＞4x+m$，得$x＜\frac{8-m}{3}$。
　又
∵不等式的解集为$x＜3$，
∴$\frac{8-m}{3}=3$，
∴$m=-1$。

6. 某次数学竞赛活动,共有20道选择题,评分办法是答对一题得5分,答错一题扣1分,不答题不得分也不扣分。某同学有一道题未答,那么这个学生至少答对17题,成绩才能在80分以上。

答案： 17　[解析]设这个学生答对了$x$道题，则答错$(20 - 1 - x)$道题，
　根据题意，得$5x-(20 - 1 - x)＞80$，
　解得$x＞\frac{33}{2}$。
　又
∵$x$为正整数，
∴$x$的最小值为17。

7. 某电器商场促销,某型号冰箱的售价是2500元,进价是1800元,商场为保证利润率不低于5%,则该型号冰箱最多降价610元。

答案： 610　[解析]设该型号冰箱降价$x$元，
　根据题意，得$2500 - 1800 - x\geq5\%×1800$，
　解得$x\leq610$。
∴该型号冰箱最多降价610元。

8. 学校准备用2000元购买名著和词典作为艺术节奖品,其中名著每套65元,词典每本40元,现已购买名著20套,问最多还能买词典多少本？

答案： 解:设还能买词典$x$本，
根据题意，得$20×65 + 40x\leq2000$，
　解得$x\leq17\frac{1}{2}$。
　答:最多还能买词典17本。

9. 为了美化校园,我校欲购进甲、乙两种工具,如果购买甲种3件,乙种2件,共需56元；如果购买甲种1件,乙种4件,共需32元。
(1)甲、乙两种工具每件各多少元？
(2)现要购买甲、乙两种工具共100件,总费用不超过1000元,那么甲种工具最多购买多少件？

答案： 解:
(1)设甲种工具每件$x$元，乙种工具每件$y$元，
　根据题意，得$\begin{cases}3x + 2y = 56\\x + 4y = 32\end{cases}$，
　解得$\begin{cases}x = 16\\y = 4\end{cases}$。
　答:甲种工具每件16元，乙种工具每件4元。
(2)设甲种工具购买了$m$件，则乙种工具购买了$(100 - m)$件，根据题意，得$16m + 4(100 - m)\leq1000$，
　解得$m\leq50$。
　答:甲种工具最多购买50件。

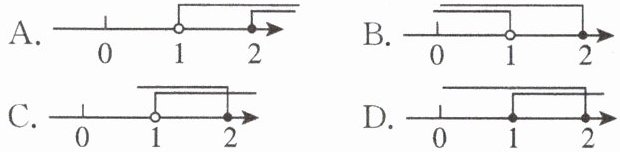
10. 不等式组$\begin{cases}x + 1 ＞ 2,\\3x - 4 \leq 2\end{cases} $的解集表示在数轴上正确的是(C)

答案： C

11. 满足不等式组$\begin{cases}2x - 1 \leq 0,\\x + 1 ＞ 0\end{cases} $的整数解是0。

答案： 0

12. 解不等式组$\begin{cases}3x ＜ x + 2,\frac{x + 1}{2} \geq \frac{2x + 1}{5},\end{cases} $并把解集在数轴上表示出来。

答案：
解:$\begin{cases}3x ＜ x + 2,①\frac{x + 1}{2}\geq\frac{2x + 1}{5},②\end{cases}$
　解不等式①，得$x ＜ 1$，
　解不等式②，得$x\geq - 3$，
　故此不等式组的解集为$-3\leq x ＜ 1$。
　在数轴上表示为