《2025年鲁人泰斗假期好时光八年级数学青岛版》

19. (10分)某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费 $ y $(元)是行李质量 $ x(kg) $ 的一次函数,已知行李质量为20kg时,需付行李费2元,行李质量为50kg时,需付行李费8元。
(1)当行李的质量 $ x $ 超过规定时,求 $ y $ 与 $ x $ 之间的函数表达式；
(2)求旅客最多可免费携带行李的质量。

答案： 19.解:
(1)根据题意,设y与x的函数表达式为y=kx+b.
当x=20时,y=2,得2=20k+b;当x=50时,y=8,得8=50k+b.
解方程组$\begin{cases}20k + b = 2\\50k + b = 8\end{cases}$,得$\begin{cases}k = \frac{1}{5}\\b = -2\end{cases}$,
∴所求函数表达式为y=$\frac{1}{5}$x−2.
(2)当y=0时,$\frac{1}{5}$x−2=0,解得x=10.
答:旅客最多可免费携带行李10kg.

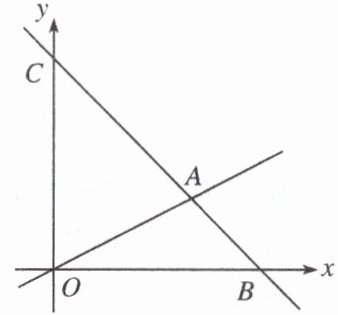
20. (12分)如图,在平面直角坐标系中,过点 $ C(0,6) $ 的直线 $ AC $ 与直线 $ OA $ 相交于点 $ A(4,2) $。
(1)求直线 $ AC $ 的表达式；y=−x+6
(2)动点 $ M $ 在线段 $ OA $ 和射线 $ AC $ 上运动,是否存在点 $ M $,使 $ \triangle OMC $ 的面积是 $ \triangle OAC $ 的面积的 $ \frac{1}{4} $？若存在,求出此时点 $ M $ 的坐标；若不存在,请说明理由。存在，点M的坐标是(1,$\frac{1}{2}$)或(1,5)或(−1,7)

答案： 20.解:
(1)设直线AC的表达式是y=kx+b,根据题意,得$\begin{cases}4k + b = 2\\b = 6\end{cases}$,解得$\begin{cases}k = -1\\b = 6\end{cases}$,则直线AC的表达式是y=−x+6.
(2)设直线OA的表达式是y=mx,则4m=2,解得m=$\frac{1}{2}$,则直线OA的表达式是y=$\frac{1}{2}$x.
∵当△OMC的面积是△OAC的面积的$\frac{1}{4}$时,
∴点M到y轴的距离是$\frac{1}{4}$×4=1.
∴点M的横坐标为1或−1;
当点M的横坐标是1时,在y=$\frac{1}{2}$x中,当x=1时,y=$\frac{1}{2}$,则点M的坐标是(1,$\frac{1}{2}$);在y=−x+6中,当x=1时,y=5,则点M的坐标是(1,5).当点M的横坐标是−1时,在y=−x+6中,当x=−1时,y=7,则点M的坐标是(−1,7).
综上所述，点M的坐标是(1,$\frac{1}{2}$)或(1,5)或(−1,7).