2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. 如图,已知$△OAB$是正三角形,$OP⊥OB,OP= OA$,将$△OAB$绕点 O 按顺时针方向旋转,使得 OA 与 OP 重合,得到$△OPQ$,则旋转的角度是
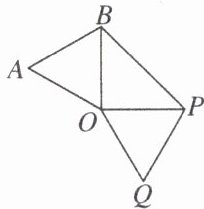
A.$60^{\circ }$
B.$90^{\circ }$
C.$120^{\circ }$
D.$150^{\circ }$
150°

A.$60^{\circ }$
B.$90^{\circ }$
C.$120^{\circ }$
D.$150^{\circ }$
答案:
6. D【解析】$\because \triangle OAB$是正三角形,
$\therefore \angle BOA=60^{\circ}$。
$\because OP\perp OB$,
$\therefore \angle BOP=90^{\circ}$。
$\therefore \angle AOP=\angle BOA+\angle BOP=60^{\circ}+90^{\circ}=150^{\circ}$,即旋转角是$150^{\circ}$。故选 D。
$\therefore \angle BOA=60^{\circ}$。
$\because OP\perp OB$,
$\therefore \angle BOP=90^{\circ}$。
$\therefore \angle AOP=\angle BOA+\angle BOP=60^{\circ}+90^{\circ}=150^{\circ}$,即旋转角是$150^{\circ}$。故选 D。
7. (
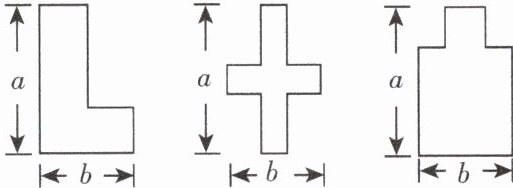
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
D
)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是
A.甲种方案所用铁丝最长
B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长
D.三种方案所用铁丝一样长
答案:
7. D
8. 如图,将$Rt△ABC$绕直角顶点 C 顺时针旋转$90^{\circ }$,得到$△A'B'C$,连接$AA'$,若$∠1= 25^{\circ }$,则$∠BAA'$的度数是
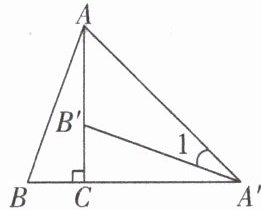
A.$55^{\circ }$
B.$60^{\circ }$
C.$65^{\circ }$
D.$70^{\circ }$
C

A.$55^{\circ }$
B.$60^{\circ }$
C.$65^{\circ }$
D.$70^{\circ }$
答案:
8. C
9. 如图,将$△ABC$沿 BC 所在的直线平移得到$△DEF$.如果$GC= 2,DF= 4.5$,那么$AG= $
2.5
.
答案:
9. $2.5$
10. 点$(a,1)与点(-2,b)$关于原点对称,则$ab= $
$-2$
.
答案:
10. $-2$
11. 如图,点 E 是正方形 ABCD 中 CD 边上的中点,$AB= 4$,把$△ADE$绕点 A 顺时针旋转$90^{\circ }得到△ABF$,若连接 EF,则$EF= $____.
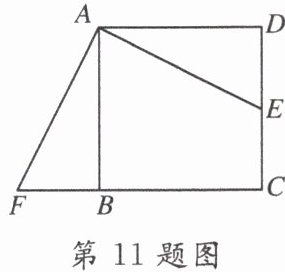

答案:
11. $2\sqrt{10}$【解析】如图,连接$EF$。
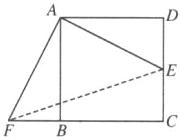
$\because$把$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle ABF$,
$\therefore AE=AF$,$\angle EAF=90^{\circ}$。
$\because$四边形$ABCD$是正方形,
$\therefore AB=CD=AD=4$。
$\because E$是$CD$的中点,
$\therefore DE=\frac{1}{2}CD=2$。
$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。
$\therefore EF=\sqrt{AE^{2}+AF^{2}}=\sqrt{(2\sqrt{5})^{2}+(2\sqrt{5})^{2}}=2\sqrt{10}$。
11. $2\sqrt{10}$【解析】如图,连接$EF$。

$\because$把$\triangle ADE$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle ABF$,
$\therefore AE=AF$,$\angle EAF=90^{\circ}$。
$\because$四边形$ABCD$是正方形,
$\therefore AB=CD=AD=4$。
$\because E$是$CD$的中点,
$\therefore DE=\frac{1}{2}CD=2$。
$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。
$\therefore EF=\sqrt{AE^{2}+AF^{2}}=\sqrt{(2\sqrt{5})^{2}+(2\sqrt{5})^{2}}=2\sqrt{10}$。
12. 如图,已知$△AOB与△DOC$成中心对称,$△AOB$的面积是 6,$AB= 4$,则$△DOC$中 CD 边上的高是____
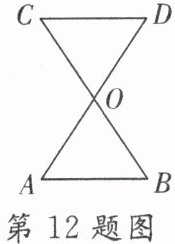
3
.
答案:
12. $3$
13. 如图,四边形 ABCD 是菱形,点 O 是两条对角线的交点,过点 O 的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为 6 和 8 时,则阴影部分的面积为____
12
.
答案:
13. $12$【解析】$\because$菱形的两条对角线的长分别为$6$和$8$,
$\therefore$菱形的面积$=\frac{1}{2}× 6× 8=24$。
$\because O$是菱形两条对角线的交点,
$\therefore$阴影部分的面积$=\frac{1}{2}× 24=12$。
$\therefore$菱形的面积$=\frac{1}{2}× 6× 8=24$。
$\because O$是菱形两条对角线的交点,
$\therefore$阴影部分的面积$=\frac{1}{2}× 24=12$。
14. 如图,在$Rt△ABC$中,$∠ACB= 90^{\circ }$,将$△ABC$绕顶点 C 逆时针旋转得到$△A'B'C$,点 M 是 BC 的中点,点 P 是$A'B'$的中点,连接 PM,若$BC= 2,∠BAC= 30^{\circ }$,则线段 PM 的最大值是____.
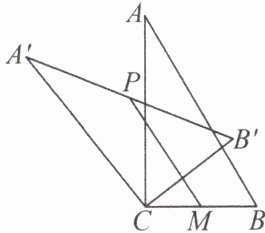

答案:
14. $3$【解析】如图,连接$PC$。
在$Rt\triangle ABC$中,$\because \angle A=30^{\circ}$,$BC=2$,
$\therefore AB=4$。
根据旋转不变性可知,$A'B'=AB=4$,
$\because$点$P$为$A'B'$的中点,
$\therefore PC=\frac{1}{2}A'B'=2$。
$\because CM=BM=1$,
且$PM\leq PC+CM$,$\therefore PM\leq 3$,
$\therefore PM$的最大值为$3$(此时$P$,$C$,$M$共线)。

14. $3$【解析】如图,连接$PC$。
在$Rt\triangle ABC$中,$\because \angle A=30^{\circ}$,$BC=2$,
$\therefore AB=4$。
根据旋转不变性可知,$A'B'=AB=4$,
$\because$点$P$为$A'B'$的中点,
$\therefore PC=\frac{1}{2}A'B'=2$。
$\because CM=BM=1$,
且$PM\leq PC+CM$,$\therefore PM\leq 3$,
$\therefore PM$的最大值为$3$(此时$P$,$C$,$M$共线)。

15. (8分)如图,在平面直角坐标系中,$△ABC三个顶点的坐标分别是A(2,4),B(1,1),C(4,3)$,请画出$△ABC关于原点对称的△A_{1}B_{1}C_{1}$,并分别写出$A_{1},B_{1},C_{1}$的坐标.
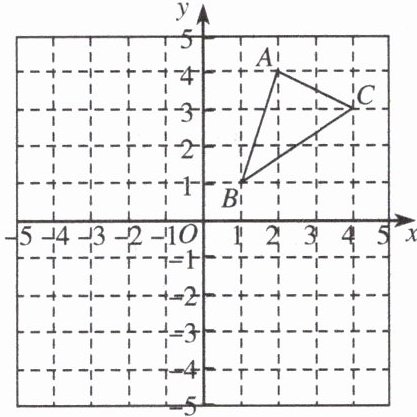

答案:
15. 解:如图所示,$\triangle A_{1}B_{1}C_{1}$即为所求,点$A_{1}$,$B_{1}$,$C_{1}$的坐标分别为$(-2,-4)$,$(-1,-1)$,$C(-4,-3)$。

15. 解:如图所示,$\triangle A_{1}B_{1}C_{1}$即为所求,点$A_{1}$,$B_{1}$,$C_{1}$的坐标分别为$(-2,-4)$,$(-1,-1)$,$C(-4,-3)$。

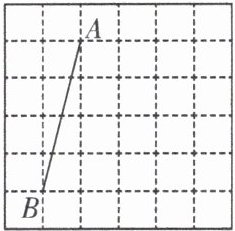
16. (8分)如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段 AB 的端点均在格点上.
(1)将线段 AB 向右平移 3 个单位长度,得到线段$A'B'$,画出平移后的线段并连接$AB'和A'B$,两线段相交于点 O;
(2)求证:$△AOB\cong △B'OA'.$
(1)将线段 AB 向右平移 3 个单位长度,得到线段$A'B'$,画出平移后的线段并连接$AB'和A'B$,两线段相交于点 O;
(2)求证:$△AOB\cong △B'OA'.$

答案:
16. 解:(1)如图所示。

(2)证明:$\because AB// A'B'$,
$\therefore \angle A=\angle B'$,$\angle B=\angle A'$。
在$\triangle AOB$和$\triangle B'OA'$中,
$\left\{\begin{array}{l}\angle A=\angle B'\\ AB=B'A'\\ \angle B=\angle A'\end{array}\right.$,
$\therefore \triangle AOB\cong \triangle B'OA'(ASA)$。
16. 解:(1)如图所示。

(2)证明:$\because AB// A'B'$,
$\therefore \angle A=\angle B'$,$\angle B=\angle A'$。
在$\triangle AOB$和$\triangle B'OA'$中,
$\left\{\begin{array}{l}\angle A=\angle B'\\ AB=B'A'\\ \angle B=\angle A'\end{array}\right.$,
$\therefore \triangle AOB\cong \triangle B'OA'(ASA)$。
查看更多完整答案,请扫码查看


