《2025年鲁人泰斗假期好时光八年级数学青岛版》

17. (10分)如图,以锐角$△ABC$的边 AC,AB 为边向外作正方形 ACDE 和正方形 ABGF,连接 BE、CF.
(1)求证:$△FAC\cong △BAE;$
证明：$\because$四边形$ABGF$和四边形$ACDE$是正方形，
$\therefore AF=AB$，$AC=AE$。
$\because \angle BAF=\angle CAE=90^{\circ}$，
$\therefore \angle BAF+\angle BAC=\angle CAE+\angle BAC$，
即$\angle FAC=\angle BAE$。
在$\triangle FAC$和$\triangle BAE$中，
$\left\{\begin{array}{l}AF=AB\\ \angle FAC=\angle BAE\\ AC=AE\end{array}\right.$，
$\therefore \triangle FAC\cong \triangle BAE$SAS。
(2)图中可以通过旋转$△BAE而得到△FAC$,请你说出旋转中心、旋转方向和旋转角的度数.
旋转中心为点A，旋转方向为顺时针，旋转角的度数为90°。

答案： 17. 解：（1）证明：$\because$四边形$ABGF$和四边形$ACDE$是正方形，
$\therefore AF=AB$，$AC=AE$。
$\because \angle BAF=\angle CAE=90^{\circ}$，
$\therefore \angle BAF+\angle BAC=\angle CAE+\angle BAC$，
即$\angle FAC=\angle BAE$。
在$\triangle FAC$和$\triangle BAE$中，
$\left\{\begin{array}{l}AF=AB\\ \angle FAC=\angle BAE\\ AC=AE\end{array}\right.$，
$\therefore \triangle FAC\cong \triangle BAE(SAS)$。
（2）以点$A$为旋转中心，将$\triangle BAE$顺时针旋转$90^{\circ}$得到$\triangle FAC$。

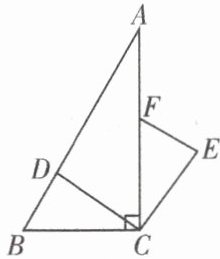
18. (10分)如图,在$Rt△ABC$中,$∠ACB= 90^{\circ }$,点 D,F 分别在 AB,AC 上,$CF= CB$,连接 CD,将线段 CD 绕点 C 按顺时针方向旋转$90^{\circ }$后得到 CE,连接 EF.
(1)求证:$△BCD\cong △FCE$;
证明：$\because CD$绕点$C$顺时针旋转$90^{\circ}$得到$CE$，$\therefore CD=CE$，$\angle DCE=90^{\circ}$。$\because \angle ACB=90^{\circ}$，$\therefore \angle BCD=90^{\circ}-\angle ACD=\angle FCE$。在$\triangle BCD$和$\triangle FCE$中，$\left\{\begin{array}{l}CB=CF\\ \angle BCD=\angle FCE\\ CD=CE\end{array}\right.$，$\therefore \triangle BCD\cong \triangle FCE$(SAS)。
(2)若$EF// CD$,求$∠BDC$的度数.90°

答案： 18. 解：（1）证明：$\because CD$绕点$C$顺时针旋转$90^{\circ}$得到$CE$，
$\therefore CD=CE$，$\angle DCE=90^{\circ}$。
$\because \angle ACB=90^{\circ}$，
$\therefore \angle BCD=90^{\circ}-\angle ACD=\angle FCE$。
在$\triangle BCD$和$\triangle FCE$中，
$\left\{\begin{array}{l}CB=CF\\ \angle BCD=\angle FCE\\ CD=CE\end{array}\right.$，
$\therefore \triangle BCD\cong \triangle FCE(SAS)$。
（2）由$\triangle BCD\cong \triangle FCE$，得$\angle BDC=\angle E$，
$\because EF// CD$，
$\therefore \angle E=180^{\circ}-\angle DCE=90^{\circ}$。$\therefore \angle BDC=90^{\circ}$。

19. (10分)如图,点 D 是等边三角形 ABC 内一点,将线段 AD 绕点 A 顺时针旋转$60^{\circ }$,得到线段 AE,连接 CD,BE.
(1)求证:$∠AEB= ∠ADC;$
(2)连接 DE,若$∠ADC= 105^{\circ }$,求$∠BED$的度数.45°

答案： 19. 解：（1）$\because \triangle ABC$是等边三角形，
$\therefore \angle BAC=60^{\circ}$，$AB=AC$。
$\because$线段$AD$绕点$A$顺时针旋转$60^{\circ}$，得到线段$AE$，
$\therefore \angle DAE=60^{\circ}$，$AE=AD$。
$\therefore \angle BAD+\angle EAB=\angle BAD+\angle DAC$。
$\therefore \angle EAB=\angle DAC$。
在$\triangle EAB$和$\triangle DAC$中，
$\left\{\begin{array}{l}AB=AC\\ \angle EAB=\angle DAC\\ AE=AD\end{array}\right.$，
$\therefore \triangle EAB\cong \triangle DAC(SAS)$。
$\therefore \angle AEB=\angle ADC$。
（2）$\because \angle DAE=60^{\circ}$，$AE=AD$，
$\therefore \triangle EAD$为等边三角形。
$\therefore \angle AED=60^{\circ}$。
又$\because \angle AEB=\angle ADC=105^{\circ}$，
$\therefore \angle BED=105^{\circ}-60^{\circ}=45^{\circ}$。

20. (12分)如图,在正方形 ABCD 中,点 E 是 AB 边上的一点(与 A,B 两点不重合),将$△BCE$绕点 C 旋转,使 CB 与 CD 重合,这时点 E 落在点 F 处,连接 EF.
(1)按照题目要求画出图形;
(2)若正方形边长为 3,$BE= 1$,求$△AEF$的面积;
(3)若正方形边长为 m,$BE= n$,比较$△AEF与△CEF$的面积大小,并说明理由.

答案：
20. 解：（1）如图，即为按照题目要求画出的图形。

（2）根据旋转的性质可知$DF=BE=1$，
$\therefore \triangle AEF$的面积$=\frac{1}{2}× AE× AF=4$。
（3）根据旋转的性质可知$DF=BE=n$，
$\therefore \triangle AEF$的面积$=\frac{1}{2}× AE× AF=\frac{1}{2}(m-n)(m+n)=\frac{1}{2}m^{2}-\frac{1}{2}n^{2}$。
$\because \triangle CBE$的面积$=\triangle CDF$的面积，
$\therefore$四边形$AECF$的面积$=$四边形$ABCD$的面积。
$\therefore S_{\triangle CEF}=S_{四边形AECF}-S_{\triangle AEF}$
$=m^{2}-(\frac{1}{2}m^{2}-\frac{1}{2}n^{2})=\frac{1}{2}m^{2}+\frac{1}{2}n^{2}$。
$\because m＞n＞0$，
$\therefore \frac{1}{2}m^{2}+\frac{1}{2}n^{2}＞\frac{1}{2}m^{2}-\frac{1}{2}n^{2}$。
$\therefore S_{\triangle CEF}＞S_{\triangle AEF}$。