2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列说法正确的是 (
A.0.01 的平方根是 0.1
B.$\sqrt{8}= 4$
C.0 的立方根是 0
D.1 的立方根是 $\pm 1$
C
)A.0.01 的平方根是 0.1
B.$\sqrt{8}= 4$
C.0 的立方根是 0
D.1 的立方根是 $\pm 1$
答案:
1. C
2. 3 的算术平方根是
$\sqrt{3}$
,27 的立方根是3
.
答案:
2. $\sqrt{3}$ 3
3. 有一个边长 11 cm 的正方形和一个长为 13 cm,宽为 8 cm 的长方形,要制作一个面积为这两个图形面积之和的正方形,该正方形的边长应为多少?
答案:
3. 解:设正方形的边长为$x$cm.
依题意,得$x^{2}=11^{2}+13×8$,
即$x^{2}=225$,
$\therefore x=15$或$x=-15$(舍去).
$\therefore$正方形的边长为15cm.
依题意,得$x^{2}=11^{2}+13×8$,
即$x^{2}=225$,
$\therefore x=15$或$x=-15$(舍去).
$\therefore$正方形的边长为15cm.
4. 下列各数中,无理数是 (
A.$\sqrt{4}$
B.$-\frac{4}{3}$
C.0.333…
D.$-\pi$
D
)A.$\sqrt{4}$
B.$-\frac{4}{3}$
C.0.333…
D.$-\pi$
答案:
4. D
5. 下列正方形中,边长为无理数的是 (
A.面积为 0.25 的正方形
B.面积为 2 的正方形
C.面积为 $\frac{9}{4}$ 的正方形
D.面积为 16 的正方形
B
)A.面积为 0.25 的正方形
B.面积为 2 的正方形
C.面积为 $\frac{9}{4}$ 的正方形
D.面积为 16 的正方形
答案:
5. B 【解析】A. 面积为0.25的正方形,其边长为0.5,是有理数,故本选项不合题意;B. 面积为2的正方形,其边长为$\sqrt{2}$,是无理数,故本选项符合题意;C. 面积为$\frac{9}{4}$的正方形,其边长为$\frac{3}{2}$,是有理数,故本选项不合题意;D. 面积为16的正方形,其边长为4,是有理数,故本选项不合题意.故选B.
6. 甲、乙两同学玩“写数游戏”:要求每人写一个无理数,并使它们的和为有理数. 若甲同学写的数为 $\sqrt{3}$,那么乙同学可写
$-\sqrt{3}$
(写出一个即可)
答案:
6. $-\sqrt{3}$
7. 估计 $\sqrt{138}$ 的大小应 (
A.在 9~10 之间
B.在 10~11 之间
C.在 11~12 之间
D.在 12~13 之间
C
)A.在 9~10 之间
B.在 10~11 之间
C.在 11~12 之间
D.在 12~13 之间
答案:
7. C
8. 计算:$(2-\sqrt{3})^0+2^{2023}×(-\frac{1}{2})^{2022}$ (
A.2
B.$\frac{1}{2}$
C.$-\frac{1}{2}$
D.3
D
)A.2
B.$\frac{1}{2}$
C.$-\frac{1}{2}$
D.3
答案:
8. D
9. 下列各数中最大的是 (
A.0.78
B.$\frac{7}{8}$
C.87%
D.$\frac{\pi}{4}$
B
)A.0.78
B.$\frac{7}{8}$
C.87%
D.$\frac{\pi}{4}$
答案:
9. B
10. 如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点 A 处,则点 A 表示的数是

$\sqrt{2}$
.
答案:
10. $\sqrt{2}$
11. 直角三角形的两直角边长分别为 6 和 8,则斜边上的中线长是 (
A.10
B.2.5
C.5
D.8
C
)A.10
B.2.5
C.5
D.8
答案:
11. C
12. 如图,以 $Rt\triangle ABC$ 的三边向外作正方形,其面积分别为 $S_1$,$S_2$,$S_3$,且 $S_1= 5$,$S_2= 12$,则 $S_3= $
17
.
答案:
12. 17
13. 下列几组数中,不能作为直角三角形的三边长的是 (
A.4,9,11
B.6,8,10
C.7,24,25
D.8,15,17
A
)A.4,9,11
B.6,8,10
C.7,24,25
D.8,15,17
答案:
13. A
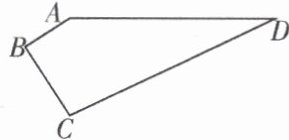
14. 如图,在四边形 ABCD 中,$AB= 3$,$BC= 4$,$CD= 13$,$AD= 12$,$∠B= 90^{\circ}$,求四边形 ABCD 的面积.

答案:
14. 解:如图,连接AC.
∵∠B=90°,

∴由勾股定理,得$AC=\sqrt{AB^{2}+BC^{2}}$
$=\sqrt{3^{2}+4^{2}}=5.\because AC^{2}+AD^{2}=25+144=169=CD^{2}$,
$\therefore △ACD$是直角三角形.
$\therefore S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=\frac{1}{2}×3×4+\frac{1}{2}×5×12$
$=6+30=36$.
14. 解:如图,连接AC.
∵∠B=90°,

∴由勾股定理,得$AC=\sqrt{AB^{2}+BC^{2}}$
$=\sqrt{3^{2}+4^{2}}=5.\because AC^{2}+AD^{2}=25+144=169=CD^{2}$,
$\therefore △ACD$是直角三角形.
$\therefore S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=\frac{1}{2}×3×4+\frac{1}{2}×5×12$
$=6+30=36$.
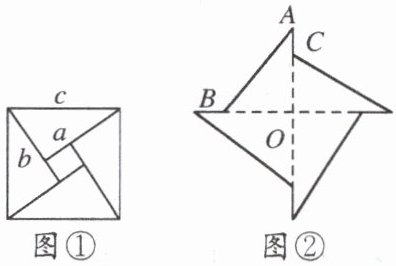
15. 如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为 a,较短的直角边为 b,斜边长为 c,结合图①,试验证勾股定理;
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为 24,$OC= 3$,求该飞镖状图案的面积.
(1)$S_{小正方形}=(a-b)^{2}=a^{2}-2ab+b^{2}$,另一方面$S_{小正方形}=c^{2}-4×\frac{1}{2}ab=c^{2}-2ab$,即$b^{2}-2ab+a^{2}=c^{2}-2ab$,则
(2)
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为 a,较短的直角边为 b,斜边长为 c,结合图①,试验证勾股定理;
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为 24,$OC= 3$,求该飞镖状图案的面积.

(1)$S_{小正方形}=(a-b)^{2}=a^{2}-2ab+b^{2}$,另一方面$S_{小正方形}=c^{2}-4×\frac{1}{2}ab=c^{2}-2ab$,即$b^{2}-2ab+a^{2}=c^{2}-2ab$,则
$a^{2}+b^{2}=c^{2}$
.(2)
24÷4=6
,设$AC=x$,依题意,有$(x+3)^{2}+3^{2}=(6-x)^{2}$,解得$x=1$
.$\therefore S_{飞镖图案}=$$\frac{1}{2}×(3+1)×3×4=24$
.
答案:
15. 解:
(1)$S_{小正方形}=(a-b)^{2}=a^{2}-2ab+b^{2}$,另一方面$S_{小正方形}=c^{2}-4×\frac{1}{2}ab=c^{2}-2ab$,即$b^{2}-2ab+a^{2}=c^{2}-2ab$,
则$a^{2}+b^{2}=c^{2}$.
(2)$24÷4=6$,
设$AC=x$,依题意,有$(x+3)^{2}+3^{2}=(6-x)^{2}$,
解得$x=1$.
$\therefore S_{飞镖图案}=\frac{1}{2}×(3+1)×3×4=24$.
(1)$S_{小正方形}=(a-b)^{2}=a^{2}-2ab+b^{2}$,另一方面$S_{小正方形}=c^{2}-4×\frac{1}{2}ab=c^{2}-2ab$,即$b^{2}-2ab+a^{2}=c^{2}-2ab$,
则$a^{2}+b^{2}=c^{2}$.
(2)$24÷4=6$,
设$AC=x$,依题意,有$(x+3)^{2}+3^{2}=(6-x)^{2}$,
解得$x=1$.
$\therefore S_{飞镖图案}=\frac{1}{2}×(3+1)×3×4=24$.
查看更多完整答案,请扫码查看


