《2025年鲁人泰斗假期好时光八年级数学青岛版》

9. 若两个相似三角形的面积比为 $9:25$,则这两个相似三角形的周长比是$3:5$.

答案： $3:5$

10. 为了测量一棵树的高度,小梦在同一时间、同一地点测得小兰身高 $1.5\mathrm{m}$,她的影长是 $2.4\mathrm{m}$,树的影子长 $4\mathrm{m}$,则这棵树高有2.5$\mathrm{m}$.

答案： $2.5$

11. 若两个相似多边形的最长边的长度分别为 $10$ 和 $20$,且其中一个多边形的最短边长为 $4$,则另一个多边形的最短边长为8或2.

答案： $8$或$2$

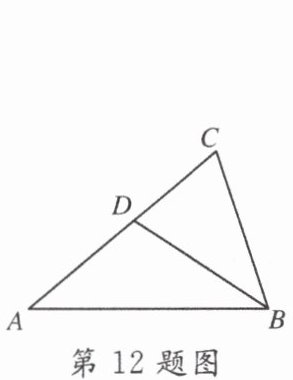
12. 如图,在 $\triangle ABC$ 中,点 $D$ 是 $AC$ 上一点,$\angle CBD = \angle A$,$\frac{BC}{AC} = \frac{2}{3}$,则 $\frac{CD}{AD}$ 的值是______$\frac {4}{5}$.

答案： $\frac {4}{5}$【解析】$\because ∠CBD=∠A,∠C=∠C$，
$\therefore \triangle ABC\backsim \triangle BDC$．
$\therefore \frac {BC}{AC}=\frac {CD}{BC}=\frac {2}{3}$．
$\therefore$ 设$CD=2x,BC=3x$．
$\because \frac {BC}{AC}=\frac {2}{3}$，
$\therefore AC=\frac {9}{2}x$．
$\therefore AD=AC - CD=\frac {5}{2}x$．
$\therefore \frac {CD}{AD}=\frac {2x}{\frac {5}{2}x}=\frac {4}{5}$．

13. 在一块直角三角形铁皮上截一块正方形铁皮,如图,已有的铁皮是 $Rt\triangle ABC$,$\angle C = 90^{\circ}$,要截得的正方形 $EFGD$ 的边 $FG$ 在 $AB$ 上,顶点 $E$,$D$ 分别在边 $CA$,$CB$ 上,如果 $AF = 4$,$BG = 9$,那么正方形铁皮的边长为______6.

答案： $6$【解析】根据题意知，$∠AFE=∠BGD=∠C=90^{\circ }$，
$\therefore ∠A=∠BDG$（同角的余角相等）．
$\therefore \triangle AEF\backsim \triangle DBG$．
$\therefore \frac {AF}{DG}=\frac {EF}{BG}$．
又$\because EF=DG,AF=4,BG=9$，
$\therefore \frac {4}{EF}=\frac {EF}{9}$．
$\therefore EF=6$，即正方形铁皮的边长为$6$．

14. 如图,在 $\triangle ABC$ 中,$AD_1 = \frac{1}{4}AB$,$D_1D_2 = \frac{1}{4}D_1B$,$D_2D_3 = \frac{1}{4}D_2B$,……,照这样继续下去,$D_{2020}D_{2021} = \frac{1}{4}D_{2020}B$,且 $D_1E_1 // BC$,$D_2E_2 // BC$,$D_3E_3 // BC$,……,$D_{2021}E_{2021} // BC$,则 $\frac{D_{2021}E_{2021}}{BC} = $______$1-(\frac {3}{4})^{2021}$.

答案： $1-(\frac {3}{4})^{2021}$【解析】$\because D_{1}E_{1}// BC$，
$\therefore \triangle AD_{1}E_{1}\backsim \triangle ABC$．
$\therefore \frac {D_{1}E_{1}}{BC}=\frac {AD_{1}}{AB}=\frac {1}{4}$．
$\therefore D_{1}E_{1}=\frac {1}{4}BC,D_{1}B=\frac {3}{4}AB$．
$\because D_{1}D_{2}=\frac {1}{4}D_{1}B=\frac {3}{16}AB$，
$\therefore AD_{2}=AD_{1}+D_{1}D_{2}=\frac {1}{4}AB+\frac {3}{16}AB=\frac {7}{16}AB$．
$\therefore D_{2}E_{2}=\frac {7}{16}BC=(1-\frac {9}{16})\cdot BC=[1-(\frac {3}{4})^{2}]\cdot BC$，
同理可得$D_{3}E_{3}=\frac {27}{64}BC=[1-(\frac {3}{4})^{3}]\cdot BC$．
$\therefore D_{n}E_{n}=[1-(\frac {3}{4})^{n}]\cdot BC$．
$\therefore \frac {D_{2021}E_{2021}}{BC}=1-(\frac {3}{4})^{2021}$．

15. (8分)如图,点 $D$ 在 $\angle BAC$ 的内部,$\angle 1 = \angle 2$,$\angle 1 + \angle BAC = 180^{\circ}$. $BD = 1.5$,$CD = 2$,求 $AD$ 的长.

答案：
解：延长$AD$，如图所示．
$\because ∠1+∠BAC=180^{\circ }$，
$∠1+∠BDE=180^{\circ }$，
$\therefore ∠BAC=∠BDE$．
又$\because ∠BAC=∠BAD+∠CAD$，
$∠BDE=∠BAD+∠B$，
$\therefore ∠B=∠CAD$．
$\because ∠1=∠2$，
$\therefore \triangle ABD\backsim \triangle CAD$．
$\therefore \frac {BD}{AD}=\frac {AD}{CD}$，即$\frac {1.5}{AD}=\frac {AD}{2}$．
$\therefore AD=\sqrt {3}$．

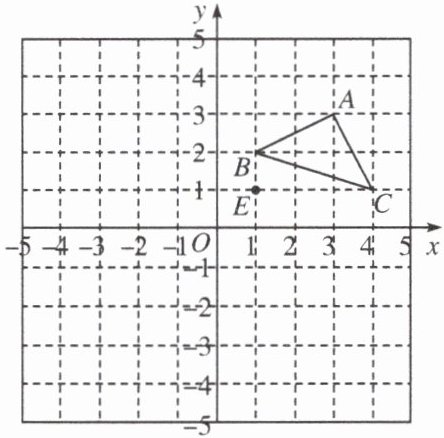
16. (8分)如图,在平面直角坐标系中,$\triangle ABC$ 三个顶点的坐标分别为 $A(3,3)$,$B(1,2)$,$C(4,1)$,点 $E$ 的坐标为 $(1,1)$.
(1)画出将 $\triangle ABC$ 向左平移 $5$ 个单位长度的 $\triangle A_1B_1C_1$；
(2)画出和 $\triangle ABC$ 以点 $E$ 为位似中心的位似图形 $\triangle A_2B_2C_2$,$\triangle A_2B_2C_2$ 和 $\triangle ABC$ 相似比为 $2:1$,且位于点 $E$ 的两侧；
(3)直接写出点 $A_2$,$B_2$,$C_2$ 三个点的坐标.

答案：
解：（1）如图，$\triangle A_{1}B_{1}C_{1}$即为所求作．

（2）如图，$\triangle A_{2}B_{2}C_{2}$即为所求作
（3）由图可知，$A_{2}(-3,-3),B_{2}(1,-1),C_{2}(-5,1)$．