2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 根据相似多边形的定义,三角分别
相等
,三边对应成比例
的两个三角形叫做相似三角形.
答案:
1.相等 对应成比例
2.
两角
分别相等的两个三角形相似.
答案:
2.两角
【典型例题 2】如图,在$\triangle ABC$中,点$D在AB$边上,$\angle ABC= \angle ACD$.求证:$\triangle ABC\backsim\triangle ACD$.


答案:
证明:在$\triangle ABC与\triangle ACD$中,
$\because \angle ABC= \angle ACD$,$\angle A= \angle A$,
$\therefore \triangle ABC\backsim\triangle ACD$.
$\because \angle ABC= \angle ACD$,$\angle A= \angle A$,
$\therefore \triangle ABC\backsim\triangle ACD$.
1. 如图,在$\triangle ABC$中,$\angle AED= \angle B$,则下列等式成立的是(
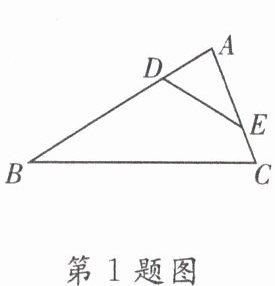
A.$\frac{DE}{BC}= \frac{AD}{DB}$
B.$\frac{AE}{BC}= \frac{AD}{BD}$
C.$\frac{DE}{CB}= \frac{AE}{AB}$
D.$\frac{AD}{AB}= \frac{AE}{AC}$
C
)
A.$\frac{DE}{BC}= \frac{AD}{DB}$
B.$\frac{AE}{BC}= \frac{AD}{BD}$
C.$\frac{DE}{CB}= \frac{AE}{AB}$
D.$\frac{AD}{AB}= \frac{AE}{AC}$
答案:
1.C [解析]
∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$=$\frac{DE}{CB}$.故选C;
∵∠AED=∠B,∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$=$\frac{DE}{CB}$.故选C;
2. 如图,已知$\triangle ABC与\triangle BDE$都是等边三角形,点$D在边AC$上(不与点$A$、$C$重合),$DE与AB相交于点F$,那么与$\triangle BFD$相似的三角形是(
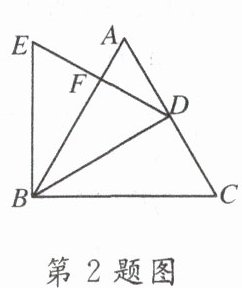
A.$\triangle BFE$
B.$\triangle BDC$
C.$\triangle BDA$
D.$\triangle AFD$
C
)
A.$\triangle BFE$
B.$\triangle BDC$
C.$\triangle BDA$
D.$\triangle AFD$
答案:
2.C [解析]
∵△ABC与△BDE都是等边三角形,
∴∠A=∠BDF=60°.
∵∠ABD=∠DBF,
∴△BFD∽△BDA.
∴与△BFD相似的三角形是△BDA.故选C.
∵△ABC与△BDE都是等边三角形,
∴∠A=∠BDF=60°.
∵∠ABD=∠DBF,
∴△BFD∽△BDA.
∴与△BFD相似的三角形是△BDA.故选C.
3. 如图,已知$\angle 1= \angle 2= \angle 3$,图中有
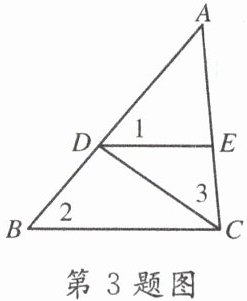
4
对相似三角形.
答案:
3.4 [解析]
∵∠A=∠A,∠1=∠2,
∴△ADE∽△ABC,
∵∠A=∠A,∠1=∠3,
∴△ADE∽△ACD.
∴△ABC∽△ACD.
∵∠1=∠2,
∴DE//BC;
∴∠EDC=∠DCB,
∵∠2=∠3,
∴△BDC∽△CED.
∵∠A=∠A,∠1=∠2,
∴△ADE∽△ABC,
∵∠A=∠A,∠1=∠3,
∴△ADE∽△ACD.
∴△ABC∽△ACD.
∵∠1=∠2,
∴DE//BC;
∴∠EDC=∠DCB,
∵∠2=∠3,
∴△BDC∽△CED.
两边
对应成比例
,且夹角
相等的两个三角形相似.
答案:
对应成比例 夹角
【典型例题 3】如图,在$\triangle ABC和\triangle ADE$中,$\angle BAD= \angle CAE$,$\angle ABC= \angle ADE$.
(1)写出图中两对相似三角形(不得添加字母和线):
(2)请分别说明两对三角形相似的理由.
①证$\triangle ABC\backsim\triangle ADE$:
②证$\triangle ABD\backsim\triangle ACE$:

(1)写出图中两对相似三角形(不得添加字母和线):
$\triangle ABC\backsim\triangle ADE$,$\triangle ABD\backsim\triangle ACE$
;(2)请分别说明两对三角形相似的理由.
①证$\triangle ABC\backsim\triangle ADE$:
$\because \angle BAD= \angle CAE$,$\therefore \angle BAD+\angle DAC= \angle CAE+\angle DAC$,即$\angle BAC= \angle DAE$。又$\because \angle ABC= \angle ADE$,$\therefore \triangle ABC\backsim\triangle ADE$
;②证$\triangle ABD\backsim\triangle ACE$:
$\because \triangle ABC\backsim\triangle ADE$,$\therefore \frac{AB}{AD}= \frac{AC}{AE}$。又$\because \angle BAD= \angle CAE$,$\therefore \triangle ABD\backsim\triangle ACE$
.
答案:
思路点拨:$\angle BAD= \angle CAE$,在此等式两边同时加$\angle DAC$,可证$\angle BAC= \angle DAE$,再结合已知中的$\angle ABC= \angle ADE$,可证$\triangle ABC\backsim\triangle ADE$;利用$\triangle ABC\backsim\triangle ADE$,可得$AB:AD = AC:AE$,再结合$\angle BAD= \angle CAE$,也可证$\triangle BAD\backsim\triangle CAE$.
解:
(1)$\triangle ABC\backsim\triangle ADE$,$\triangle ABD\backsim\triangle ACE$.
(2)①证$\triangle ABC\backsim\triangle ADE$,$\because \angle BAD= \angle CAE$,$\therefore \angle BAD+\angle DAC= \angle CAE+\angle DAC$,即$\angle BAC= \angle DAE$.又$\because \angle ABC= \angle ADE$,$\therefore \triangle ABC\backsim\triangle ADE$.
②证$\triangle ABD\backsim\triangle ACE$,$\because \triangle ABC\backsim\triangle ADE$,$\therefore \frac{AB}{AD}= \frac{AC}{AE}$.又$\because \angle BAD= \angle CAE$,$\therefore \triangle ABD\backsim\triangle ACE$.
解:
(1)$\triangle ABC\backsim\triangle ADE$,$\triangle ABD\backsim\triangle ACE$.
(2)①证$\triangle ABC\backsim\triangle ADE$,$\because \angle BAD= \angle CAE$,$\therefore \angle BAD+\angle DAC= \angle CAE+\angle DAC$,即$\angle BAC= \angle DAE$.又$\because \angle ABC= \angle ADE$,$\therefore \triangle ABC\backsim\triangle ADE$.
②证$\triangle ABD\backsim\triangle ACE$,$\because \triangle ABC\backsim\triangle ADE$,$\therefore \frac{AB}{AD}= \frac{AC}{AE}$.又$\because \angle BAD= \angle CAE$,$\therefore \triangle ABD\backsim\triangle ACE$.
1. 如图,$\angle 1= \angle 2$,则下列各式不能说明$\triangle ABC\backsim\triangle ADE$的是(

A.$\angle D= \angle B$
B.$\frac{AD}{AB}= \frac{DE}{BC}$
C.$\frac{AD}{AB}= \frac{AE}{AC}$
D.$\angle E= \angle C$
B
)
A.$\angle D= \angle B$
B.$\frac{AD}{AB}= \frac{DE}{BC}$
C.$\frac{AD}{AB}= \frac{AE}{AC}$
D.$\angle E= \angle C$
答案:
1.B [解析]
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
A和D符合有两组角对应相等的两个三角形相似;B.对应边成比例但无法证明其夹角相等,故其不能推出两三角形相似;C.符合两组对应边的比相等且夹角相等的两个三角形相似,故选B.
∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠BAC.
A和D符合有两组角对应相等的两个三角形相似;B.对应边成比例但无法证明其夹角相等,故其不能推出两三角形相似;C.符合两组对应边的比相等且夹角相等的两个三角形相似,故选B.
查看更多完整答案,请扫码查看


