《2025年鲁人泰斗假期好时光八年级数学青岛版》

20. 如图,点$E$,$F分别在菱形ABCD的边DC$,$DA$上,且$CE = AF$。求证：$\angle ABF = \angle CBE$。
证明：∵ 四边形ABCD是菱形，
∴ AB = CB，∠A = ∠C.
在 △ABF 和 △CBE 中，
{AF = CE,
∠A = ∠C,
AB = CB,
∴ △ABF ≌ △CBESAS.
∴ ∠ABF = ∠CBE.

答案： 证明：
∵ 四边形ABCD是菱形，
∴ AB = CB，∠A = ∠C.
在 △ABF 和 △CBE 中，
{AF = CE,
∠A = ∠C,
AB = CB,
∴ △ABF ≌ △CBE(SAS).
∴ ∠ABF = ∠CBE.

21. 下列条件中,不能判定一个四边形是菱形的是(B)
A.一组邻边相等的平行四边形
B.一条对角线平分一组对角的四边形
C.四条边都相等的四边形
D.对角线互相垂直平分的四边形

答案： B 【解析】A.
∵ 一组邻边相等的平行四边形是菱形，
∴ 此选项不符合题意；B.
∵ 一条对角线平分一组对角的四边形不一定是菱形，
∴ 此选项符合题意；C.
∵ 四条边都相等的四边形是菱形，
∴ 此选项不符合题意；D.
∵ 对角线互相垂直平分的四边形是菱形，
∴ 此选项不符合题意. 故选B.

22. 如图,在$□ ABCD$中,点$E$,$F分别在边AD$,$BC$上,且$DE = BF$,则再添加一个条件：______AE = AF可判定四边形$AFCE$是菱形。(只添加一个条件)

答案： AE = AF 【解析】
∵ 四边形ABCD是平行四边形，
∴ AD//BC，且 AD = BC.
又
∵ DE = BF，
∴ AE = CF.
∴ 四边形AFCE是平行四边形.
又
∵ AE = AF，
∴ 四边形AFCE是菱形.

23. 已知：如图,在四边形$ABCD$中,$AB// CD$,$CD = \frac{1}{2}AB$,$AD\perp BD$,点$E为AB$的中点。求证：四边形$BCDE$是菱形。

答案： 证明：
∵ E为AB的中点，
∴ BE = $\frac{1}{2}$AB.
∵ CD = $\frac{1}{2}$AB，
∴ BE = CD.
又
∵ AB//CD，
∴ 四边形BCDE是平行四边形.
∵ AD⊥BD，
∴ ∠ADB = 90°.
∵ E为AB的中点，
∴ DE = $\frac{1}{2}$AB = BE.
∴ 四边形BCDE是菱形.

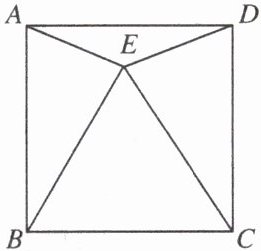
24. 如图,四边形$ABCD$是正方形,$\triangle CBE$是等边三角形,则$\angle AEB = $75°。

答案： 75° 【解析】
∵ 四边形ABCD是正方形，△CBE是等边三角形，
∴ AB = BC，∠ABC = 90°，BE = BC，∠EBC = 60°.
∴ AB = BE，∠ABE = 30°.
∴ ∠AEB = $\frac{1}{2}$(180° - 30°) = 75°.

25. 如图,四边形$ABCD$是正方形,$E$,$F分别是AB$,$AD$上的一点,且$BF\perp CE$,垂足为$G$。
求证：$AF = BE$。
证明：∵ 四边形ABCD是正方形，
∴ AB = BC，∠A = ∠CBE = 90°.
∵ BF⊥CE，
∴ ∠BCE + ∠CBG = 90°.
∵ ∠ABF + ∠CBG = 90°.
∴ ∠BCE = ∠ABF.
在 △BCE 和 △ABF 中，
{∠BCE = ∠ABF,
BC = AB,
∠CBE = ∠A,
∴ △BCE ≌ △ABF(ASA).
∴ BE = AF.

答案： 证明：
∵ 四边形ABCD是正方形，
∴ AB = BC，∠A = ∠CBE = 90°.
∵ BF⊥CE，
∴ ∠BCE + ∠CBG = 90°.
∵ ∠ABF + ∠CBG = 90°.
∴ ∠BCE = ∠ABF.
在 △BCE 和 △ABF 中，
{∠BCE = ∠ABF,
BC = AB,
∠CBE = ∠A,
∴ △BCE ≌ △ABF(ASA).
∴ BE = AF.

26. 下列说法中错误的是(A)
A.对角线相等的矩形是正方形
B.对角线互相平分的四边形是平行四边形
C.对角线垂直的矩形是正方形
D.对角线互相平分且相等的四边形是矩形

答案： A 【解析】对角线相等的矩形不一定是正方形，如一组邻边长为2和3的矩形，它的对角线相等，但不是正方形，故选项A错误；对角线互相平分的四边形是平行四边形，故选项B正确；对角线垂直的矩形是正方形，故选项C正确；对角线互相平分且相等的四边形是矩形，故选项D正确. 故选A.

27. 如图,在$\triangle ABC$中,$AC = BC$,点$D$、$E分别是边AB$、$AC$的中点。延长$DE到点F$,使$DE = EF$,得四边形$ADCF$。当$\angle ACB = $90°时,四边形$ADCF$是正方形。

答案： 90° 【解析】
∵ AC = BC，∠ACB = 90°，
∴ ∠CAB = ∠CBA = 45°.
∵ AC = BC，D为AB的中点，
∴ CD⊥AB，CD平分 ∠ACB.
∴ ∠ADC = 90°，∠ACD = $\frac{1}{2}$∠ACB = $\frac{1}{2}$× 90° = 45° = ∠CAB.
∴ AD = CD.
∵ E为AC的中点，
∴ AE = CE.
∵ DE = EF，
∴ 四边形ADCF是平行四边形.
∵ ∠CDA = 90°，AD = CD，
∴ 四边形ADCF是正方形.
即当 ∠ACB = 90° 时，四边形ADCF是正方形.

28. $\triangle ABC$中,$AB = 7$,$BC = 6$,$AC = 5$,点$D$、$E$、$F$分别是三边的中点,则$\triangle DEF$的周长为(9)
A.4.5
B.9
C.10
D.12

答案： B 【解析】
∵ 点D、E、F分别是三边的中点，
∴ DE、EF、DF为 △ABC的中位线.
∴ EF = $\frac{1}{2}$AB = $\frac{1}{2}$× 7 = $\frac{7}{2}$，DE = $\frac{1}{2}$AC = $\frac{1}{2}$× 5 = $\frac{5}{2}$，DF = $\frac{1}{2}$BC = $\frac{1}{2}$× 6 = 3.
∴ △DEF的周长 = $\frac{7}{2}$ + $\frac{5}{2}$ + 3 = 9.

29. 如图,$A$,$B$两点被池塘隔开,不能直接测量其距离。于是,小明在岸边选一点$C$,连接$CA$,$CB$,分别延长到点$M$,$N$,使$AM = AC$,$BN = BC$,测得$MN = 200m$,则$A$,$B$间的距离为______100$m$。

答案： 100

30. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,点$D$,$E分别是AB$,$AC$的中点,点$F是AD$的中点。若$AB = 8$,则$EF = $2。

答案： 2