《2025年鲁人泰斗假期好时光八年级数学青岛版》

13. 关于$x的一元一次不等式\frac{m - 2x}{3} \leq -2的解集为x \geq 4$,则$m$的值为(2)
A.14
B.7
C.-2
D.2

答案： D　[解析]
∵$\frac{m - 2x}{3}\leq - 2$，
∴$m - 2x\leq - 6$，
∴$-2x\leq - m - 6$，
∴$x\geq\frac{1}{2}m + 3$。
∵关于$x$的一元一次不等式$\frac{m - 2x}{3}\leq - 2$的解集为$x\geq4$，
∴$\frac{1}{2}m + 3 = 4$，解得$m = 2$。故选D。

14. 若不等式组$\begin{cases}1 + x ＞ a,\\2x - 4 ＜ 0\end{cases} $有解,则$a$的取值范围是(B)
A.$a \leq 3$
B.$a ＜ 3$
C.$a ＜ 2$
D.$a \leq 2$

答案： B

15. 若关于$x的不等式组\begin{cases}x - 2 ＜ 0,\\3x + 4 ＞ a - x\end{cases} $恰好只有2个整数解,则所有满足条件的整数$a$的值之和是(C)
A.3
B.4
C.6
D.1

答案： C　[解析]解不等式组，得$\frac{a - 4}{4}＜x＜2$，
　　由关于$x$的不等式组$\begin{cases}x - 2 ＜ 0\\3x + 4 ＞ a - x\end{cases}$恰好只有2个整数解，得到$-1\leq\frac{a - 4}{4}＜0$，即$0\leq a ＜ 4$。
　满足条件的整数$a$的值为0，1，2，3，
　整数$a$的值之和是$0 + 1 + 2 + 3 = 6$。故选C。

16. 为更好地推进生活垃圾分类工作,改善城市生态环境,市政府召开了生活垃圾分类推进会,意味着垃圾分类战役的全面打响。某小区准备购买A、B两种型号的垃圾箱,通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元。
(1)每个A型垃圾箱和B型垃圾箱分别是多少元？
(2)若该小区物业计划用低于2150元的资金购买A,B两种型号的垃圾箱共20个,且至少购买6个B型垃圾箱,请问有几种购买方案？

答案： 解:
(1)设每个A型垃圾箱$x$元，每个B型垃圾箱$y$元，根据题意，得$\begin{cases}3x + 2y = 540\\3y - 2x = 160\end{cases}$，
　解得$\begin{cases}x = 100\\y = 120\end{cases}$。
　答:每个A型垃圾箱100元，每个B型垃圾箱120元。
(2)设购买$m$个B型垃圾箱，则购买$(20 - m)$个A型垃圾箱，
　根据题意，得$\begin{cases}m\geq6\\100(20 - m)+120m ＜ 2150\end{cases}$，
　解得$6\leq m＜\frac{15}{2}$。
　又
∵$m$为整数，
∴$m$可以为6，7。
∴有2种购买方案。

1. 若 $ 3x ＞ -3y $,则下列不等式中一定成立的是(A)
A.$ x + y ＞ 0 $
B.$ x - y ＞ 0 $
C.$ x + y ＜ 0 $
D.$ x - y ＜ 0 $

答案： A

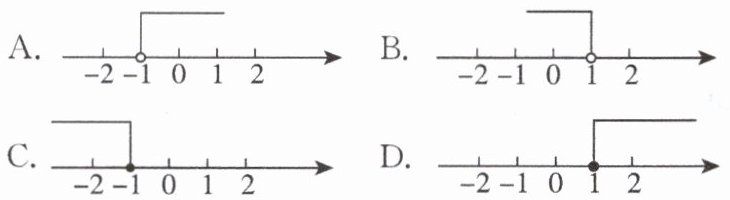
2. 不等式 $ 2x + 3 \geq 5 $ 的解集在数轴上表示正确的是(D)

答案： D

3. 下列不等式说法中,不正确的是(B)
A.若 $ x ＞ y $,$ y ＞ 2 $,则 $ x ＞ 2 $
B.若 $ x ＞ y $,则 $ x - 2 ＜ y - 2 $
C.若 $ x ＞ y $,则 $ 2x ＞ 2y $
D.若 $ x ＞ y $,则 $ -2x - 2 ＜ -2y - 2 $

答案： B【解析】A. $\because x＞y,y＞2,\therefore x＞2$，原说法正确，故本选项不符合题意；B. $\because x＞y,\therefore x - 2＞y - 2$，原说法错误，故本选项符合题意；C. $\because x＞y,\therefore 2x＞2y$，原说法正确，故本选项不符合题意；D. $\because x＞y,\therefore -2x - 2＜-2y - 2$，原说法正确，故本选项不符合题意。故选 B。

4. 若点 $ P(2m - 3, -m) $ 在第四象限,则 $ m $ 的取值范围是(C)
A.$ 0 ＜ m ＜ \frac{3}{2} $
B.$ m ＞ 0 $
C.$ m ＞ \frac{3}{2} $
D.$ m ＜ 0 $

答案： C

5. 若 $ 0 ＜ m ＜ 1 $, $ m $、$ m^2 $、$ \frac{1}{m} $ 的大小关系是(B)
A.$ m ＜ m^2 ＜ \frac{1}{m} $
B.$ m^2 ＜ m ＜ \frac{1}{m} $
C.$ \frac{1}{m} ＜ m ＜ m^2 $
D.$ \frac{1}{m} ＜ m^2 ＜ m $

答案： B

6. 若不等式组 $ \begin{cases} 4x - 3(x + a) \geq 0, \\ \frac{3x + 1}{2} - \frac{1}{4}(x - 1) ＜ 0 \end{cases} $ 有 3 个整数解,则 $ a $ 的取值范围是(B)
A.$ -\frac{4}{3} \leq a ＜ -1 $
B.$ -\frac{4}{3} ＜ a \leq -1 $
C.$ -\frac{3}{5} ＜ a \leq 3 $
D.$ -\frac{3}{5} \leq a ＜ 3 $

答案： B【解析】解不等式$4x - 3(x + a)\geqslant 0$，得$x\geqslant 3a$，解不等式$\frac {3x + 1}{2}-\frac {1}{4}(x - 1)＜0$，得$x＜-\frac {3}{5}$，$\therefore$不等式组的解集为$3a\leqslant x＜-\frac {3}{5}$。$\because$不等式组有 3 个整数解，$\therefore$不等式组的 3 个整数解为$-3,-2,-1$，$\therefore -4＜3a\leqslant -3$，$\therefore a$的取值范围为$-\frac {4}{3}＜a\leqslant -1$，故选 B。

7. 已知 $ x = 2 $ 是不等式组 $ (x - 5)(ax - 3a + 2) \leq 0 $ 的解,且 $ x = 1 $ 不是这个不等式的解,则实数 $ a $ 的取值范围是(C)
A.$ a ＞ 1 $
B.$ a \leq 2 $
C.$ 1 ＜ a \leq 2 $
D.$ 1 \leq a \leq 2 $

答案： C

8. 某市出租车的收费标准是：起步价 8 元(即行驶距离不超过 3 千米都需付 8 元车费),超过 3 千米以后,每增加 1 千米,加收 1.5 元(不足 1 千米按 1 千米计)。某人从甲地到乙地经过的路程是 $ x $ 千米,出租车费为 15.5 元,那么 $ x $ 的最大值是(B)
A.11
B.8
C.7
D.5

答案： B