2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知$\triangle ABC的各边长分别为2$,$5$,$6$,与其相似的另一个$\triangle A'B'C'的最大边为18$,则$\triangle ABC与\triangle A'B'C'$的面积比等于(
A.$1:3$
B.$1:6$
C.$1:9$
D.$4:9$
C
)A.$1:3$
B.$1:6$
C.$1:9$
D.$4:9$
答案:
C [解析]
∵△ABC的各边长分别为2,5,6,与其相似的另一个△A'B'C'的最大边为18,
∴两三角形的相似比为6:18=1:3.
∴△ABC与△A'B'C'的面积比=(1:3)²=1:9.故选C.
∵△ABC的各边长分别为2,5,6,与其相似的另一个△A'B'C'的最大边为18,
∴两三角形的相似比为6:18=1:3.
∴△ABC与△A'B'C'的面积比=(1:3)²=1:9.故选C.
2. 如图,在$\triangle ABC$中,点$D$,$E分别是AB$,$AC$的中点,连接$DE$。过点$D作DF\perp BC于点F$,连接$EF$。若$\triangle DEF的面积为1$,则四边形$DECB$的面积为( )
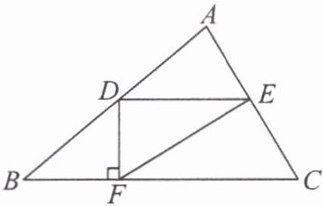
A.$5$
B.$4$
C.$3$
D.$2$

A.$5$
B.$4$
C.$3$
D.$2$
答案:
C [解析]如图,作AM⊥BC于点M,交DE于点N,
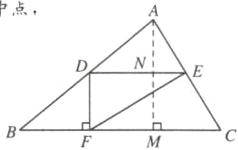
∵点D,E分别是AB,AC的中点,
∴DE//BC,DE=$\frac{1}{2}$BC.
∴△ADE∽△ABC.
∴AN=$\frac{1}{2}$AM.
∴△ADE的面积=△DEF的面积=1.
∵△ADE∽△ABC,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}$=($\frac{1}{2}$)²=$\frac{1}{4}$
∴△ABC的面积=4.
∴四边形DECB的面积=4−1=3.
故选C.
C [解析]如图,作AM⊥BC于点M,交DE于点N,

∵点D,E分别是AB,AC的中点,
∴DE//BC,DE=$\frac{1}{2}$BC.
∴△ADE∽△ABC.
∴AN=$\frac{1}{2}$AM.
∴△ADE的面积=△DEF的面积=1.
∵△ADE∽△ABC,
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}$=($\frac{1}{2}$)²=$\frac{1}{4}$
∴△ABC的面积=4.
∴四边形DECB的面积=4−1=3.
故选C.
3. 已知$\triangle ABC\backsim\triangle DEF$,$\frac{DE}{AB}= \frac{2}{3}$,$\triangle ABC的周长是12cm$,面积是$30cm^{2}$。
(1) 求$\triangle DEF$的周长;
(2) 求$\triangle DEF$的面积。
(1) 求$\triangle DEF$的周长;
8cm
(2) 求$\triangle DEF$的面积。
$\frac{40}{3}cm^{2}$
答案:
解:
(1)
∵$\frac{DE}{AB}$=$\frac{2}{3}$,
∴△DEF的周长=12×$\frac{2}{3}$=8(cm).
(2)
∵$\frac{DE}{AB}$=$\frac{2}{3}$,
∴△DEF的面积=30×($\frac{2}{3}$)²=$\frac{40}{3}$(cm²).
(1)
∵$\frac{DE}{AB}$=$\frac{2}{3}$,
∴△DEF的周长=12×$\frac{2}{3}$=8(cm).
(2)
∵$\frac{DE}{AB}$=$\frac{2}{3}$,
∴△DEF的面积=30×($\frac{2}{3}$)²=$\frac{40}{3}$(cm²).
1. 已知$\triangle ABC\backsim\triangle DEF$,$AB = 3$,$DE = 5$,则$\triangle ABC与\triangle DEF$的面积之比为(
A.$\frac{9}{25}$
B.$\frac{3}{5}$
C.$\frac{5}{3}$
D.$\frac{25}{9}$
A
)A.$\frac{9}{25}$
B.$\frac{3}{5}$
C.$\frac{5}{3}$
D.$\frac{25}{9}$
答案:
A
2. 如图,已知$\triangle ABC\backsim\triangle DEF$,$AB:DE = 1:2$,则下列等式一定成立的是(
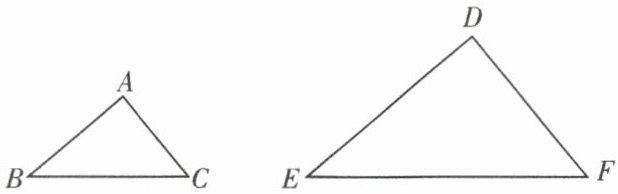
A.$\frac{BC}{DF}= \frac{1}{2}$
B.$\frac{\angle A的度数}{\angle D的度数}= \frac{1}{2}$
C.$\frac{\triangle ABC的面积}{\triangle DEF的面积}= \frac{1}{2}$
D.$\frac{\triangle ABC的周长}{\triangle DEF的周长}= \frac{1}{2}$
D
)
A.$\frac{BC}{DF}= \frac{1}{2}$
B.$\frac{\angle A的度数}{\angle D的度数}= \frac{1}{2}$
C.$\frac{\triangle ABC的面积}{\triangle DEF的面积}= \frac{1}{2}$
D.$\frac{\triangle ABC的周长}{\triangle DEF的周长}= \frac{1}{2}$
答案:
D
3. 已知$\triangle ABC与\triangle DEF$相似,又有$\angle A = 40^{\circ}$,$\angle B = 60^{\circ}$,那么$\angle D$不可能是(
A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$100^{\circ}$
D
)A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$100^{\circ}$
答案:
D
4. 如图,已知在$\triangle ABC$中,点$D$,$E是边BC$上的两点,连接$AD$,$AE$,且$AD = AE$,如果$\triangle ABE\backsim\triangle CBA$,那么下列等式错误的是(
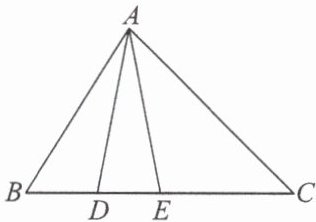
A.$AB^{2}= BE\cdot BC$
B.$CD\cdot AB = AD\cdot AC$
C.$AE^{2}= CD\cdot BE$
D.$AB\cdot AC = BE\cdot CD$
D
)
A.$AB^{2}= BE\cdot BC$
B.$CD\cdot AB = AD\cdot AC$
C.$AE^{2}= CD\cdot BE$
D.$AB\cdot AC = BE\cdot CD$
答案:
D [解析]
∵△ABE∽△CBA,
∴AB:CB=BE:BA.
∴AB²=BE·BC.故A选项的结论正确;
∵△ABE∽△CBA,
∴∠BAE=∠C,∠AEB=∠CAB.
∵AD=AE,
∴∠ADE=∠AED.
∴∠ADE=∠CAB.
∵∠ACD=∠BCA,
∴△CAD∽△CBA.
∴CD:CA=AD:BA,
即CD·AB=AD·AC.故B选项的结论正确;
∵△ABE∽△CBA,△CAD∽△CBA,
∴△CAD∽△ABE,
∴AD:BE=CD:AE,
即AD·AE=CD·BE.
∵AD=AE,
∴AE²=CD·BE.故C选项的结论正确;
∵△ABE∽△CBA,
∴AB:CB=EA:AC.
∴AB·AC=EA·CB,
∵AE²=CD·BE,AE≠CB,
∴AB·AC≠BE·CD.故D选项的结论不正确.故选D.
∵△ABE∽△CBA,
∴AB:CB=BE:BA.
∴AB²=BE·BC.故A选项的结论正确;
∵△ABE∽△CBA,
∴∠BAE=∠C,∠AEB=∠CAB.
∵AD=AE,
∴∠ADE=∠AED.
∴∠ADE=∠CAB.
∵∠ACD=∠BCA,
∴△CAD∽△CBA.
∴CD:CA=AD:BA,
即CD·AB=AD·AC.故B选项的结论正确;
∵△ABE∽△CBA,△CAD∽△CBA,
∴△CAD∽△ABE,
∴AD:BE=CD:AE,
即AD·AE=CD·BE.
∵AD=AE,
∴AE²=CD·BE.故C选项的结论正确;
∵△ABE∽△CBA,
∴AB:CB=EA:AC.
∴AB·AC=EA·CB,
∵AE²=CD·BE,AE≠CB,
∴AB·AC≠BE·CD.故D选项的结论不正确.故选D.
查看更多完整答案,请扫码查看


