《2025年鲁人泰斗假期好时光八年级数学青岛版》

2. 在$\triangle ABC和\triangle DEF$中,$\frac{AB}{DE}= \frac{BC}{EF}$.要使$\triangle ABC\backsim\triangle DEF$,还需要添加一个条件,那么这个条件可以是______∠B=∠E(答案不唯一,只需填写一个正确的答案).

答案： 2.∠B=∠E　(答案不唯一).

3. 已知：点$P是正方形ABCD的边BC$上的点,且$BP = 3PC$,$Q是CD$的中点,求证：$\triangle ADQ\backsim\triangle QCP$.

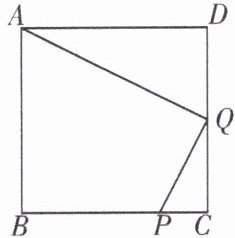
证明:在正方形ABCD中,
　∵Q是CD的中点，∴$\frac{AD}{QC}$=2.
　∵$\frac{BP}{PC}$=3,∴$\frac{BC}{PC}$=4.
　又∵BC=2DQ,∴$\frac{DQ}{PC}$=2.
　在△ADQ和△QCP中,$\frac{AD}{QC}$=$\frac{DQ}{CP}$,∠C=∠D=90°,
　∴△ADQ∽△QCP.

答案： 3.证明:在正方形ABCD中,
∵Q是CD的中点，
∴$\frac{AD}{QC}$=2.
∵$\frac{BP}{PC}$=3,
∴$\frac{BC}{PC}$=4.
　又
∵BC=2DQ,
∴$\frac{DQ}{PC}$=2.
　在△ADQ和△QCP中,$\frac{AD}{QC}$=$\frac{DQ}{CP}$,∠C=∠D=90°,
∴△ADQ∽△QCP.

三边对应成比例的两个三角形相似.

答案： 对应成比例

【典型例题 4】如图,$D$,$E$,$F分别是\triangle ABC的三边BC$,$CA$,$AB$的中点.

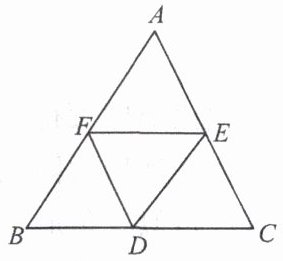
(1)求证：$\triangle DEF\backsim\triangle ABC$；
证明：$\because D$,$F分别是\triangle ABC的边BC$,$BA$的中点,
$\therefore DF= \frac{1}{2}AC$.
同理$EF= \frac{1}{2}BC$,$DE= \frac{1}{2}AB$,
则$\frac{DF}{AC}= \frac{EF}{BC}= \frac{DE}{AB}$,
$\therefore \triangle DEF\backsim\triangle ABC$.
(2)图中还有哪几对三角形相似？
$\triangle AFE\backsim\triangle ABC$,$\triangle FBD\backsim\triangle ABC$,$\triangle EDC\backsim\triangle ABC$

答案： 思路点拨：根据三角形中位线的性质可得$DF= \frac{1}{2}AC$,易得$\triangle BDF\backsim\triangle BCA$,同理可得$\triangle AFE\backsim\triangle ABC$,$\triangle CDE\backsim\triangle CBA$,根据有三边对应成比例的三角形相似,可得$\triangle DEF\backsim\triangle ABC$.
解：
(1)证明：$\because D$,$F分别是\triangle ABC的边BC$,$BA$的中点,
$\therefore DF= \frac{1}{2}AC$.
同理$EF= \frac{1}{2}BC$,$DE= \frac{1}{2}AB$,
则$\frac{DF}{AC}= \frac{EF}{BC}= \frac{DE}{AB}$,
$\therefore \triangle DEF\backsim\triangle ABC$.
(2)$\because E$,$F分别是\triangle ABC的边AC$,$AB$的中点,
$\therefore EF// BC$.
$\therefore \triangle AFE\backsim\triangle ABC$.
同理,$\triangle FBD\backsim\triangle ABC$,$\triangle EDC\backsim\triangle ABC$
$\therefore图中还有的相似三角形是\triangle AFE\backsim\triangle ABC$,$\triangle FBD\backsim\triangle ABC$,$\triangle EDC\backsim\triangle ABC$.

1. 已知$\triangle ABC的三边长分别为6cm$,$7.5cm$,$9cm$,$\triangle DEF的一边长为4cm$,当$\triangle DEF$的另两边长是下列哪一组时,这两个三角形相似(C)
A.$2cm$,$3cm$
B.$4cm$,$5cm$
C.$5cm$,$6cm$
D.$6cm$,$7cm$

答案： 1.C　[解析]设△DEF的另两边为xcm,ycm.
　若△DEF中为4cm边长的对应边为6cm,
　则$\frac{4}{6}$=$\frac{x}{7.5}$=$\frac{y}{9}$,解得x=5,y=6;
　若△DEF中为4cm边长的对应边为7.5cm,
　则$\frac{4}{7.5}$=$\frac{x}{6}$=$\frac{y}{9}$,解得x=3.2,y=4.8;
　若△DEF中为4cm边长的对应边为9cm,
　则$\frac{4}{9}$=$\frac{x}{6}$=$\frac{y}{7.5}$,解得x=$\frac{8}{3}$,y=$\frac{10}{3}$.故选C.

2. 下列条件中,不能判断$\triangle ABC与\triangle DEF$相似的是(B)
A.$\angle A= \angle D$,$\angle B= \angle F$
B.$\frac{BC}{EF}= \frac{AC}{DF}且\angle B= \angle D$
C.$\frac{AB}{DE}= \frac{BC}{EF}= \frac{AC}{DF}$
D.$\frac{AB}{DE}= \frac{AC}{DF}且\angle A= \angle D$

答案： 2.B　[解析]A.∠A=∠D、∠B=∠F,可以得出△ABC∽△DFE,故此选项不合题意;B.$\frac{BC}{EF}$=$\frac{AC}{DF}$且∠B=∠D,不是两边成比例且夹角相等，故此选项符合题意;C.$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$,可以得出△ABC∽△DEF,故此选项不合题意;D.$\frac{AB}{DE}$=$\frac{AC}{DF}$且∠A=∠D,可以得出△ABC∽△DEF,故此选项不合题意，故选B.