2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
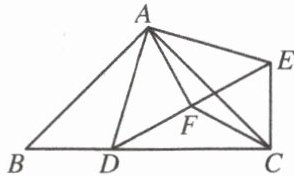
9. 如图,在Rt△ABC中,∠BAC= 90°,AB= AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE。点F是DE的中点,连接AF,CF。
(1)求证:CF= AF;
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形。
(1)求证:CF= AF;
(2)在不添加任何辅助线的情况下,请直接写出图中所有的等腰直角三角形。
△ABC,△ADE,△ADF,△AFE

答案:
9.解:
(1)证明:
∵∠BAC=∠DAE=90°,
∴∠BAC−∠CAD=∠DAE−∠CAD,
即∠BAD=∠CAE.
在△BAD与△CAE中,
$\left\{\begin{array}{l}AB = AC, \\\angle BAD = \angle CAE, \\AD = AE,\end{array}\right.$
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∴∠ABD=∠ACE=45°.
∴∠DCE=∠ACB+∠ACE=90°.
∵点F是DE的中点,∠DAE=∠DCE=90°,
∴AF=$\frac{1}{2}$DE,CF=$\frac{1}{2}$DE.
∴CF=AF.
(2)符合条件的等腰直角三角形有△ABC,△ADE,△ADF,△AFE.理由如下:
在△ABC中,AB=AC,∠BAC=90°,则△ABC是等腰直角三角形.
在△ADE中,AD=AE,∠DAE=90°,则△DEA是等腰直角三角形.
在等腰Rt△ADE中,
∵点F是DE的中点,
∴AF⊥DE,AF=DF=EF=$\frac{1}{2}$DE,
∴△ADF,△AFE都是等腰直角三角形.
(1)证明:
∵∠BAC=∠DAE=90°,
∴∠BAC−∠CAD=∠DAE−∠CAD,
即∠BAD=∠CAE.
在△BAD与△CAE中,
$\left\{\begin{array}{l}AB = AC, \\\angle BAD = \angle CAE, \\AD = AE,\end{array}\right.$
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°.
∴∠ABD=∠ACE=45°.
∴∠DCE=∠ACB+∠ACE=90°.
∵点F是DE的中点,∠DAE=∠DCE=90°,
∴AF=$\frac{1}{2}$DE,CF=$\frac{1}{2}$DE.
∴CF=AF.
(2)符合条件的等腰直角三角形有△ABC,△ADE,△ADF,△AFE.理由如下:
在△ABC中,AB=AC,∠BAC=90°,则△ABC是等腰直角三角形.
在△ADE中,AD=AE,∠DAE=90°,则△DEA是等腰直角三角形.
在等腰Rt△ADE中,
∵点F是DE的中点,
∴AF⊥DE,AF=DF=EF=$\frac{1}{2}$DE,
∴△ADF,△AFE都是等腰直角三角形.
10. 在平面直角坐标系中,点(3,-5)关于原点对称的点是(
A.(3,-5)
B.(-3,5)
C.(5,-3)
D.(-3,-5)
B
)A.(3,-5)
B.(-3,5)
C.(5,-3)
D.(-3,-5)
答案:
10.B
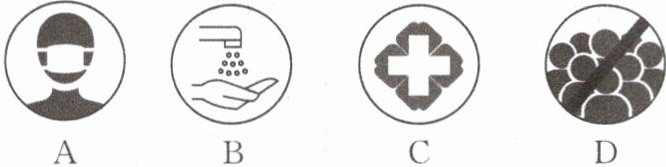
11. 下列关于防范肺炎的标志中既是轴对称图形,又是中心对称图形的是(
C
)
答案:
11.C [解析]A是轴对称图形,不是中心对称图形,故此选项不合题意;B不是轴对称图形,也不是中心对称图形,故此选项不合题意;C既是轴对称图形,又是中心对称图形,故此选项符合题意;D不是轴对称图形,也不是中心对称图形,故此选项不合题意,故选C.
12. 下列语句判断正确的是(
A.等边三角形是轴对称图形,但不是中心对称图形
B.等边三角形既是轴对称图形,又是中心对称图形
C.等边三角形是中心对称图形,但不是轴对称图形
D.等边三角形既不是轴对称图形,也不是中心对称图形
A
)A.等边三角形是轴对称图形,但不是中心对称图形
B.等边三角形既是轴对称图形,又是中心对称图形
C.等边三角形是中心对称图形,但不是轴对称图形
D.等边三角形既不是轴对称图形,也不是中心对称图形
答案:
12.A
13. 如图,矩形ABCD与矩形AB'C'D'关于点A成中心对称,试判定四边形BDB'D'的形状
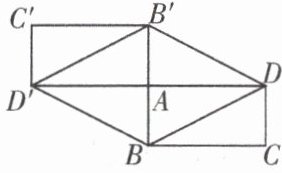
菱形
,并说明你的理由。
答案:
13.解:四边形BDB'D'是菱形.理由如下:
∵矩形ABCD与矩形AB'C'D'关于点A成中心对称,
∴∠BAD=90°,AB=AB',AD=AD'.
∴四边形BDB'D'是平行四边形.
又
∵DD'⊥BB',
∴四边形BDB'D'是菱形.
∵矩形ABCD与矩形AB'C'D'关于点A成中心对称,
∴∠BAD=90°,AB=AB',AD=AD'.
∴四边形BDB'D'是平行四边形.
又
∵DD'⊥BB',
∴四边形BDB'D'是菱形.
(
A
)1. 下列是有关防疫的图片,其中是中心对称图形的是
答案:
1. A
2. 已知点$M(a,-2)$与点$N(3,b)$关于原点对称,则$a^{b}$的值是
A.-1
B.1
C.-6
D.9
D
A.-1
B.1
C.-6
D.9
答案:
2. D
3. 如图所示,$△DEF是由△ABC$经过平移得到的,则平移的距离可能是
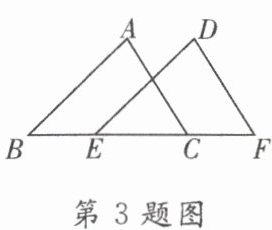
A.线段 BC 的长度
B.线段 EC 的长度
C.线段 BE 的长度
D.线段 BF 的长度
C

A.线段 BC 的长度
B.线段 EC 的长度
C.线段 BE 的长度
D.线段 BF 的长度
答案:
3. C
4. 如图,将周长为 6 cm 的$△ABC$沿 BC 方向向右平移 1 cm 得到$△DEF$,则四边形 ABFD 的周长为
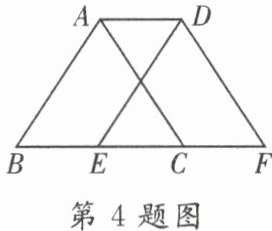
A.5 cm
B.8 cm
C.7 cm
D.6 cm
8cm

A.5 cm
B.8 cm
C.7 cm
D.6 cm
答案:
4. B【解析】$\because \triangle ABC$沿$BC$方向向右平移$1cm$得到$\triangle DEF$,
$\therefore AC=DF$,$AD=CF=1cm$。
$\because \triangle ABC$的周长为$6cm$,
$\therefore$四边形$ABFD$的周长$=AB+BC+CF+DF+AD=AB+BC+AC+CF+AD=6+1+1=8(cm)$。故选 B。
$\therefore AC=DF$,$AD=CF=1cm$。
$\because \triangle ABC$的周长为$6cm$,
$\therefore$四边形$ABFD$的周长$=AB+BC+CF+DF+AD=AB+BC+AC+CF+AD=6+1+1=8(cm)$。故选 B。
$5. $把点$P(x,y)$绕原点顺时针旋转$270^{\circ },$点$ P $的对应点的坐标是
A.$(y,-x)$
B.$(-x,-y)$
C.$(-y,x)$
D.$(x,y)$
A.$(y,-x)$
B.$(-x,-y)$
C.$(-y,x)$
D.$(x,y)$
答案:
5. C【解析】如图,不妨设点$P$在第一象限,作$PE\perp x$轴于点$E$,$P'F\perp x$轴于点$F$。

$\because$点$P'$是由点$P$绕点$O$顺时针旋转$270^{\circ}$得到,
$\therefore \angle POP'=90^{\circ}$。
$\because \angle P'FO=\angle PEO=90^{\circ}$,
$\therefore \angle P'OF+\angle POE=90^{\circ}$,$\angle P+\angle POE=90^{\circ}$。
$\therefore \angle P=\angle P'OF$。
在$\triangle POE$和$\triangle OP'F$中,
$\left\{\begin{array}{l}\angle PEO=\angle OFP'\\ \angle P=\angle P'OF\\ OP=OP'\end{array}\right.$,
$\therefore \triangle POE\cong \triangle OP'F(AAS)$。
$\therefore OE=P'F=x$,$PE=OF=y$。
$\therefore P'(-y,x)$。故选 C。
5. C【解析】如图,不妨设点$P$在第一象限,作$PE\perp x$轴于点$E$,$P'F\perp x$轴于点$F$。

$\because$点$P'$是由点$P$绕点$O$顺时针旋转$270^{\circ}$得到,
$\therefore \angle POP'=90^{\circ}$。
$\because \angle P'FO=\angle PEO=90^{\circ}$,
$\therefore \angle P'OF+\angle POE=90^{\circ}$,$\angle P+\angle POE=90^{\circ}$。
$\therefore \angle P=\angle P'OF$。
在$\triangle POE$和$\triangle OP'F$中,
$\left\{\begin{array}{l}\angle PEO=\angle OFP'\\ \angle P=\angle P'OF\\ OP=OP'\end{array}\right.$,
$\therefore \triangle POE\cong \triangle OP'F(AAS)$。
$\therefore OE=P'F=x$,$PE=OF=y$。
$\therefore P'(-y,x)$。故选 C。
查看更多完整答案,请扫码查看


