2025年鲁人泰斗假期好时光八年级数学青岛版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年鲁人泰斗假期好时光八年级数学青岛版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 若$\triangle ABC\backsim\triangle DEF$,相似比为$3:2$,则对应高的比为(
A.$3:2$
B.$3:5$
C.$9:4$
D.$4:9$
A
)A.$3:2$
B.$3:5$
C.$9:4$
D.$4:9$
答案:
A
2. 如图,$AB// DE$,$BC// DF$,已知$AF:BF = m:n$,$BC = a$,那么$CE$等于(

A.$\frac{am}{n}$
B.$\frac{an}{m}$
C.$\frac{am}{m + n}$
D.$\frac{an}{m + n}$
$\frac{na}{m+n}$
)
A.$\frac{am}{n}$
B.$\frac{an}{m}$
C.$\frac{am}{m + n}$
D.$\frac{an}{m + n}$
答案:
D [解析]
∵BC//DF,
∴$\frac{BF}{AF}$=$\frac{CD}{AD}$=$\frac{n}{m}$.
∴$\frac{CD}{AC}$=$\frac{BF}{BF+AF}$=$\frac{n}{m+n}$,
∵AB//DE,
∴△DEC∽△ABC.
∴$\frac{CE}{CB}$=$\frac{CD}{AC}$.
∴$\frac{CE}{BC}$=$\frac{BF}{BF+AF}$.
∴CE=$\frac{na}{m+n}$.故选D.
∵BC//DF,
∴$\frac{BF}{AF}$=$\frac{CD}{AD}$=$\frac{n}{m}$.
∴$\frac{CD}{AC}$=$\frac{BF}{BF+AF}$=$\frac{n}{m+n}$,
∵AB//DE,
∴△DEC∽△ABC.
∴$\frac{CE}{CB}$=$\frac{CD}{AC}$.
∴$\frac{CE}{BC}$=$\frac{BF}{BF+AF}$.
∴CE=$\frac{na}{m+n}$.故选D.
3. 如图,$\triangle ABC$是一张锐角三角形的硬纸片,$AD是边BC$上的高,$BC = 40cm$,$AD = 30cm$,从这张硬纸片上剪下一个长$HG是宽HE的2倍的矩形EFGH$,使它的一边$EF在BC$上,顶点$G$,$H分别在AC$,$AB$上,$AD与HG的交点为点M$。
(1) 求证:$\frac{AM}{AD}= \frac{HG}{BC}$;
(2) 求这个矩形$EFGH$的周长。

(1)证明:∵四边形EFGH为矩形,
∴EF//GH.
∴∠AHG=∠B.
又∵∠HAG=∠BAC,
∴△AHG∽△ABC;
∴$\frac{AM}{AD}$=$\frac{HG}{BC}$.
(2)设HE=x,则HG=2x,AM=AD−DM=AD−HE=30−x,由(1),得$\frac{30−x}{30}$=$\frac{2x}{40}$,
解得x=12,2x=24.
∴矩形EFGH的周长为
(1) 求证:$\frac{AM}{AD}= \frac{HG}{BC}$;
(2) 求这个矩形$EFGH$的周长。

(1)证明:∵四边形EFGH为矩形,
∴EF//GH.
∴∠AHG=∠B.
又∵∠HAG=∠BAC,
∴△AHG∽△ABC;
∴$\frac{AM}{AD}$=$\frac{HG}{BC}$.
(2)设HE=x,则HG=2x,AM=AD−DM=AD−HE=30−x,由(1),得$\frac{30−x}{30}$=$\frac{2x}{40}$,
解得x=12,2x=24.
∴矩形EFGH的周长为
72
cm.
答案:
解:
(1)证明:
∵四边形EFGH为矩形,
∴EF//GH.
∴∠AHG=∠B.
又
∵∠HAG=∠BAC,
∴△AHG∽△ABC;
∴$\frac{AM}{AD}$=$\frac{HG}{BC}$.
(2)设HE=x,则HG=2x,AM=AD−DM=AD−HE=30−x,由
(1),得$\frac{30−x}{30}$=$\frac{2x}{40}$,
解得x=12,2x=24.
∴矩形EFGH的周长为2×(12+24)=72(cm).
(1)证明:
∵四边形EFGH为矩形,
∴EF//GH.
∴∠AHG=∠B.
又
∵∠HAG=∠BAC,
∴△AHG∽△ABC;
∴$\frac{AM}{AD}$=$\frac{HG}{BC}$.
(2)设HE=x,则HG=2x,AM=AD−DM=AD−HE=30−x,由
(1),得$\frac{30−x}{30}$=$\frac{2x}{40}$,
解得x=12,2x=24.
∴矩形EFGH的周长为2×(12+24)=72(cm).
【典型例题2】
某生活小区的居民筹集资金$1600$元,计划在一块上、下两底分别为$10m$,$20m$的梯形空地上种植花木,如图所示,$AD// BC$,$AC与BD相交于点M$。他们在$\triangle AMD和\triangle BMC$上种植太阳花,单价为$8元/m^{2}$,当$\triangle AMD$上种满花后,花了$160$元,请计算种满$\triangle BMC$所需的费用。
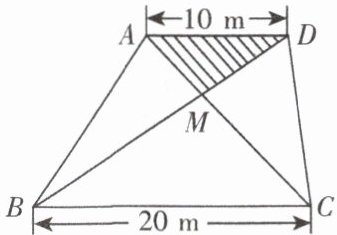
解:$\because四边形ABCD$是梯形,$AD// BC$,$\therefore\triangle AMD\backsim\triangle CMB$。
$\therefore\frac{S_{\triangle AMD}}{S_{\triangle CMB}}= (\frac{AD}{BC})^{2}= \frac{1}{4}$。
$\because种满\triangle AMD花费160$元,
$\therefore种满\triangle BMC所需的费用为160×4 =
某生活小区的居民筹集资金$1600$元,计划在一块上、下两底分别为$10m$,$20m$的梯形空地上种植花木,如图所示,$AD// BC$,$AC与BD相交于点M$。他们在$\triangle AMD和\triangle BMC$上种植太阳花,单价为$8元/m^{2}$,当$\triangle AMD$上种满花后,花了$160$元,请计算种满$\triangle BMC$所需的费用。

解:$\because四边形ABCD$是梯形,$AD// BC$,$\therefore\triangle AMD\backsim\triangle CMB$。
$\therefore\frac{S_{\triangle AMD}}{S_{\triangle CMB}}= (\frac{AD}{BC})^{2}= \frac{1}{4}$。
$\because种满\triangle AMD花费160$元,
$\therefore种满\triangle BMC所需的费用为160×4 =
640
$(元)。
答案:
思路点拨:由四边形$ABCD$是梯形,$AD// BC$,可得$\triangle AMD与\triangle CMB$相似,进而根据面积比等于相似比的平方,求出两个三角形的面积比,结合已知中$\triangle AMD$上种满花后,花了$160$元,即可得到种满$\triangle BMC$时所需的费用。
解:$\because四边形ABCD$是梯形,$AD// BC$,$\therefore\triangle AMD\backsim\triangle CMB$。
$\therefore\frac{S_{\triangle AMD}}{S_{\triangle CMB}}= (\frac{AD}{BC})^{2}= \frac{1}{4}$。
$\because种满\triangle AMD花费160$元,
$\therefore种满\triangle BMC所需的费用为160×4 = 640$(元)。
解:$\because四边形ABCD$是梯形,$AD// BC$,$\therefore\triangle AMD\backsim\triangle CMB$。
$\therefore\frac{S_{\triangle AMD}}{S_{\triangle CMB}}= (\frac{AD}{BC})^{2}= \frac{1}{4}$。
$\because种满\triangle AMD花费160$元,
$\therefore种满\triangle BMC所需的费用为160×4 = 640$(元)。
查看更多完整答案,请扫码查看


