第99页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
10. (2023·眉山)如图,AB 切⊙O 于点 B,连接 OA 交⊙O 于点 C,BD//OA 交⊙O 于点 D,连接 CD。若∠OCD = 25°,则∠A =(
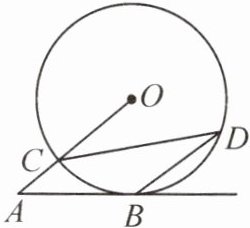
A.25°
B.35°
C.40°
D.45°
C
)
A.25°
B.35°
C.40°
D.45°
答案:
C
11. (2024·包头)如图,四边形 ABCD 是⊙O 的内接四边形,点 O 在四边形 ABCD 内部,过点 C 作⊙O 的切线交 AB 的延长线于点 P,连接 OA,OB。若∠AOB = 140°,∠BCP = 35°,则∠ADC 的度数为
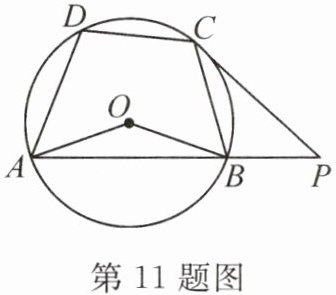
105°
。
答案:
105°
12. (2023·河南)如图,PA 与⊙O 相切于点 A,PO 交⊙O 于点 B,点 C 在 PA 上,且 CB = CA。若 OA = 5,PA = 12,则 CA 的长为
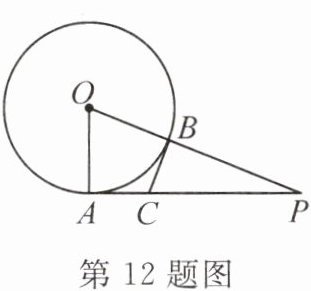
$\frac{10}{3}$
。
答案:
$\frac{10}{3}$
13. 新考向 数学文化 中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”。“方田一段,一角圆池占之。”意思是说:“一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切)”,如图所示。
问题:此图中,正方形一条对角线 AB 与⊙O 相交于点 M,N(点 N 在点 M 的右上方)。若 AB 的长度为 10 丈,⊙O 的半径为 2 丈,则 BN 的长度为
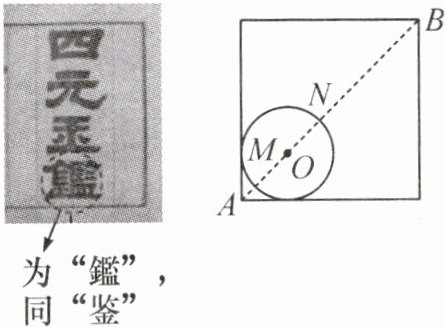
问题:此图中,正方形一条对角线 AB 与⊙O 相交于点 M,N(点 N 在点 M 的右上方)。若 AB 的长度为 10 丈,⊙O 的半径为 2 丈,则 BN 的长度为
$(8-2\sqrt{2})$
丈。
答案:
$(8-2\sqrt{2})$
14. (2023·南昌青山湖区期末)如图,BD 是⊙O 的直径,A 是 BD 延长线上的一点,点 E 在⊙O 上,BC⊥AE,交 AE 的延长线于点 C,BC 交⊙O 于点 F,且点 E 是$\overset{\frown}{DF}$的中点。
(1)求证:AC 是⊙O 的切线。
(2)若 AD = 3,AE = 3√{2},求⊙O 的半径。
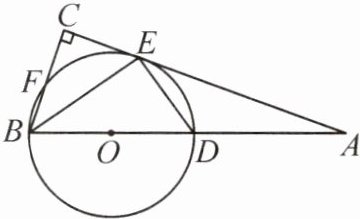
(1)求证:AC 是⊙O 的切线。
(2)若 AD = 3,AE = 3√{2},求⊙O 的半径。

答案:
解:
(1)证明:连接OE.
∵AE⊥BC,
∴∠EBC+∠BEC=90°.
∵OB=OE,
∴∠DBE=∠BEO.
∵点E是$\overset{\frown}{DF}$的中点,
∴∠EBC=∠DBE=∠BEO.
∴∠BEO+∠BEC=90°,即∠OEC=90°.
∴OE⊥AC.又
∵OE为⊙O的半径,
∴AC为⊙O的切线.
(2)设⊙O的半径为r.
∵AC为⊙O的切线,
∴∠OEC=90°.在Rt△AOE中,$AE^{2}+OE^{2}=AO^{2}$,
∴$(3\sqrt{2})^{2}+r^{2}=(3+r)^{2}$,解得r=1.5.
∴⊙O的半径为1.5.
(1)证明:连接OE.
∵AE⊥BC,
∴∠EBC+∠BEC=90°.
∵OB=OE,
∴∠DBE=∠BEO.
∵点E是$\overset{\frown}{DF}$的中点,
∴∠EBC=∠DBE=∠BEO.
∴∠BEO+∠BEC=90°,即∠OEC=90°.
∴OE⊥AC.又
∵OE为⊙O的半径,
∴AC为⊙O的切线.
(2)设⊙O的半径为r.
∵AC为⊙O的切线,
∴∠OEC=90°.在Rt△AOE中,$AE^{2}+OE^{2}=AO^{2}$,
∴$(3\sqrt{2})^{2}+r^{2}=(3+r)^{2}$,解得r=1.5.
∴⊙O的半径为1.5.
15. 如图,等边三角形 ABC 的边长为 4,⊙C 的半径为√{3},P 为 AB 边上一动点,过点 P 作⊙C 的切线 PQ,切点为 Q,则 PQ 的最小值为
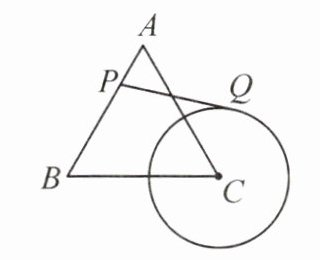
3
。
答案:
3
16. (2023·赣州赣县区期末)如图,已知⊙P 的半径是 1,圆心 P 在抛物线 $ y = \frac{1}{2}x^2 - x - \frac{1}{2} $ 上运动,当⊙P 与 x 轴相切时,圆心 P 的坐标为
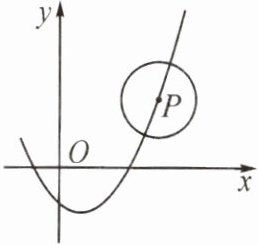
(3,1)或(-1,1)或(1,-1)
。
答案:
(3,1)或(-1,1)或(1,-1)
查看更多完整答案,请扫码查看


