《2025年名校课堂九年级数学上册人教版江西专版》

1. (2024·江科附中月考改编)下列函数中,不是二次函数的是 (D)

A.$ y = 6x^{2} + 1 $
B.$ y = -\frac{x^{2}}{8} - 1 $
C.$ y = 3x^{2} + 2x - 1 $
D.$ y = (x + 1)^{2} - x^{2} $

答案： D

2. (1)若 $ y = (m + 3)x^{2} + 4 $ 是关于 $ x $ 的二次函数,则 $ m $ 的取值范围是$m\neq -3$.
(2)若 $ y = x^{a - 1} + 2x $ 是关于 $ x $ 的二次函数,则 $ a = $3.

答案： 2.
(1)$m\neq -3$
(2)3

3. 已知二次函数 $ y = x^{2} + 3x - 2 $.
(1)当 $ x = -1 $ 时,$ y = $$-4$.
(2)当 $ y = 2 $ 时,$ x = $1或$-4$.

答案： 3.
(1)$-4$
(2)1或$-4$

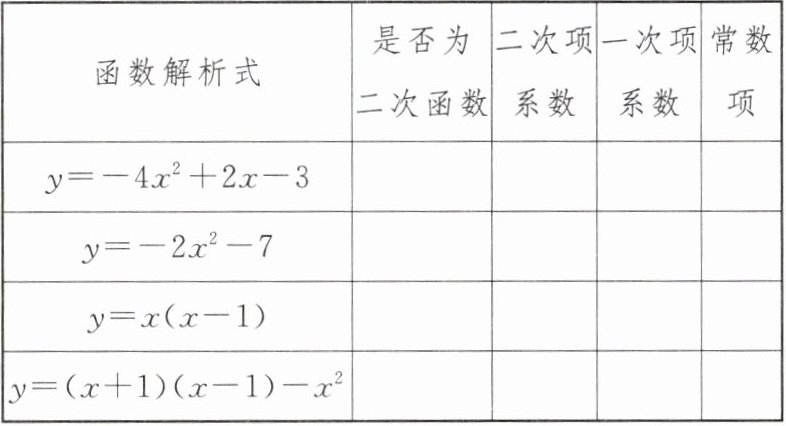
4. 判断下列函数是否为二次函数,若是二次函数,分别写出它们的二次项系数、一次项系数和常数项.

答案： 1. 是；-4；2；-3
2. 是；-2；0；-7
3. 是；1；-1；0
4. 否；无；无；无

5. (教材 P28 问题 2 变式)为方便市民进行垃圾分类投放,某环保公司第一个月投放 1000 个垃圾桶,计划第三个月投放 $ y $ 个垃圾桶,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为 $ x $,那么 $ y $ 与 $ x $ 之间的函数关系式是 (B)

A.$ y = 1000(1 - x)^{2} $
B.$ y = 1000(1 + x)^{2} $
C.$ y = (1 - x)^{2} + 1000 $
D.$ y = x^{2} + 1000 $

答案： 5.B

6. 如图,用 16 m 长的篱笆围成矩形生物园饲养小兔,设围成的矩形生物园的长为 $ x $ m,则围成的矩形生物园的面积 $ S(m^{2}) $ 与 $ x $ 的函数解析式是$S=-x^{2}+8x$.(不要求写自变量 $ x $ 的取值范围)

答案： 6.$S=-x^{2}+8x$

7. 已知一个菱形两条对角线的长度之和为 24 cm,设其中一条对角线的长为 $ x $ cm,菱形的面积为 $ S $ $ cm^{2} $,则 $ S(cm^{2}) $ 与 $ x(cm) $ 之间的函数关系式为$S=-\dfrac{1}{2}x^{2}+12x$,自变量 $ x $ 的取值范围是$0＜x＜24$.

答案： 7.$S=-\dfrac{1}{2}x^{2}+12x$ $0＜x＜24$

8. (教材 P28 问题 1 变式)某校九(1)班共有 $ x $ 名学生,在毕业典礼上每两名同学都握一次手,共握手 $ y $ 次,试写出 $ y $ 与 $ x $ 之间的函数关系式,并判断 $ y $ 是不是 $ x $ 的二次函数.

答案： ①从$x$名学生中任选$2$名学生所有可能出现的结果数为：$C_{x}^{2}=\frac{x(x - 1)}{2}$。
因为每两名同学都握一次手，所以握手总次数$y$与学生人数$x$之间的函数关系式为$y = \frac{x(x - 1)}{2}$，即$y=\frac{1}{2}x^{2}-\frac{1}{2}x$。
②根据二次函数的定义：形如$y = ax^{2}+bx + c$（$a\neq0$，$a$、$b$、$c$是常数）的函数叫做二次函数，在$y=\frac{1}{2}x^{2}-\frac{1}{2}x$中，$a = \frac{1}{2}\neq0$，$b = -\frac{1}{2}$，$c = 0$，符合二次函数的定义，所以$y$是$x$的二次函数。
综上，函数关系式为$y=\frac{1}{2}x^{2}-\frac{1}{2}x$，$y$是$x$的二次函数。

9. 已知 $ y = (m + 2)x^{|m|} + 2 $ 是关于 $ x $ 的二次函数,那么 $ m $ 的值为2.

答案： 9.2