第103页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,$\odot O$是$\triangle ABC$的内切圆,则点$O$是$\triangle ABC$的(
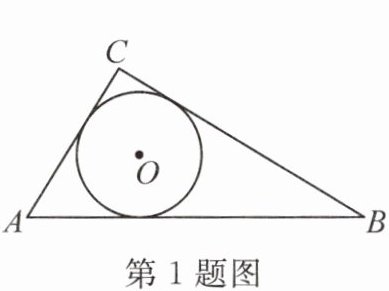
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
B
)
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
答案:
B
2. 如图,点$O$是$\triangle ABC$的内切圆的圆心. 若$\angle A = 80^{\circ}$,则$\angle BOC$的度数为

130°
.
答案:
130°
3. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3$,$BC = 4$,则$\triangle ABC$的内切圆半径$r =$
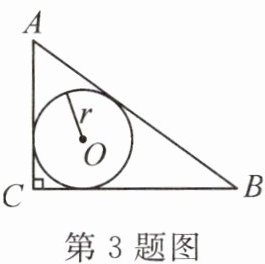
1
.
答案:
1
4. 【方程思想】(教材 P100 例 2 变式)如图,$\triangle ABC$的内切圆$\odot O$与$BC$,$CA$,$AB$分别相切于点$D$,$E$,$F$,且$AB = 18$,$BC = 28$,$CA = 26$,则$AF$的长为

8
.
答案:
8
5. 如图,已知$\triangle ABC$.
(1)尺规作图:用直尺和圆规作出$\triangle ABC$内切圆的圆心$O$.(只保留作图痕迹,不写作法和证明)
(2)如果$\triangle ABC$的周长为$14\mathrm{cm}$,内切圆的半径为$1.3\mathrm{cm}$,则$\triangle ABC$的面积为

(1)尺规作图:用直尺和圆规作出$\triangle ABC$内切圆的圆心$O$.(只保留作图痕迹,不写作法和证明)
(2)如果$\triangle ABC$的周长为$14\mathrm{cm}$,内切圆的半径为$1.3\mathrm{cm}$,则$\triangle ABC$的面积为
9.1
$\mathrm{cm}^{2}$.
答案:
1. (1)
作图步骤:
作$\angle BAC$的平分线$AD$;
作$\angle ABC$的平分线$BE$;
$AD$与$BE$相交于点$O$,则点$O$就是$\triangle ABC$内切圆的圆心(作图痕迹:以$A$为圆心,适当长为半径画弧,交$AB$、$AC$于两点,再分别以这两点为圆心,大于两点间距离一半的长为半径画弧,两弧相交于一点,过$A$与这个交点作射线$AD$;同理作$\angle ABC$的平分线$BE$)。
2. (2)
解:
根据三角形面积公式$S = S_{\triangle AOB}+S_{\triangle BOC}+S_{\triangle AOC}$。
设$\triangle ABC$三边分别为$a$,$b$,$c$,已知内切圆半径$r = 1.3\mathrm{cm}$,周长$l=a + b + c=14\mathrm{cm}$。
由$S_{\triangle AOB}=\frac{1}{2}cr$,$S_{\triangle BOC}=\frac{1}{2}ar$,$S_{\triangle AOC}=\frac{1}{2}br$。
则$S=\frac{1}{2}(a + b + c)r$(这是根据三角形内切圆的性质推导出来的公式,三角形面积等于三角形周长与内切圆半径乘积的一半)。
把$l = 14\mathrm{cm}$,$r = 1.3\mathrm{cm}$代入公式$S=\frac{1}{2}lr$,得$S=\frac{1}{2}×14×1.3$。
先计算$\frac{1}{2}×14 = 7$,再计算$7×1.3=9.1(\mathrm{cm}^{2})$。
所以$\triangle ABC$的面积为$9.1\mathrm{cm}^{2}$。
作图步骤:
作$\angle BAC$的平分线$AD$;
作$\angle ABC$的平分线$BE$;
$AD$与$BE$相交于点$O$,则点$O$就是$\triangle ABC$内切圆的圆心(作图痕迹:以$A$为圆心,适当长为半径画弧,交$AB$、$AC$于两点,再分别以这两点为圆心,大于两点间距离一半的长为半径画弧,两弧相交于一点,过$A$与这个交点作射线$AD$;同理作$\angle ABC$的平分线$BE$)。
2. (2)
解:
根据三角形面积公式$S = S_{\triangle AOB}+S_{\triangle BOC}+S_{\triangle AOC}$。
设$\triangle ABC$三边分别为$a$,$b$,$c$,已知内切圆半径$r = 1.3\mathrm{cm}$,周长$l=a + b + c=14\mathrm{cm}$。
由$S_{\triangle AOB}=\frac{1}{2}cr$,$S_{\triangle BOC}=\frac{1}{2}ar$,$S_{\triangle AOC}=\frac{1}{2}br$。
则$S=\frac{1}{2}(a + b + c)r$(这是根据三角形内切圆的性质推导出来的公式,三角形面积等于三角形周长与内切圆半径乘积的一半)。
把$l = 14\mathrm{cm}$,$r = 1.3\mathrm{cm}$代入公式$S=\frac{1}{2}lr$,得$S=\frac{1}{2}×14×1.3$。
先计算$\frac{1}{2}×14 = 7$,再计算$7×1.3=9.1(\mathrm{cm}^{2})$。
所以$\triangle ABC$的面积为$9.1\mathrm{cm}^{2}$。
6. (2023·南昌雷式学校月考)如图,点$I$为$\triangle ABC$的内心,$AB = 4$,$AC = 3$,$BC = 2$,将$\angle ACB$平移,使其顶点与点$I$重合,则图中阴影部分的周长为(
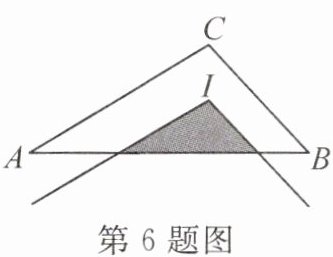
A.$4.5$
B.$4$
C.$3$
D.$2$
B
)
A.$4.5$
B.$4$
C.$3$
D.$2$
答案:
B
7. 如图,$\triangle ABC$的周长为$20\mathrm{cm}$,$BC = 6\mathrm{cm}$,$\odot O$是$\triangle ABC$的内切圆,$\odot O$的切线$MN$分别与$AB$,$CA$相交于点$M$,$N$,则$\triangle AMN$的周长为

8
$\mathrm{cm}$.
答案:
8
8. 如图,$PA$,$PB$分别与$\odot O$相切于点$A$,$B$,$BC$为$\odot O$的直径,$OP$交$\odot O$于点$E$,交$AB$于点$F$. 求证:
(1)$AC// OP$.
(2)点$E$是$\triangle ABP$的内心.
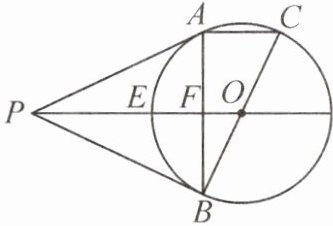
(1)$AC// OP$.
(2)点$E$是$\triangle ABP$的内心.

答案:
证明:
(1)
∵PA,PB是⊙O的切线,
∴PA=PB,∠APO=∠BPO.
∴PO⊥AB.
∴∠AFP=90°.
∵BC为⊙O的直径,
∴∠BAC=90°.
∴∠BAC=∠AFP=90°.
∴AC//OP.
(2)连接BE.
∵PB是⊙O的切线,
∴∠PBO=90°.
∴∠PBE+∠OBE=90°.
∵PF⊥AB,
∴∠EBF+∠BEF=90°.
∵OB=OE,
∴∠BEF=∠OBE.
∴∠PBE=∠EBF.
∴BE平分∠PBF.
∵PA,PB是⊙O的切线,
∴PO平分∠APB.
∴点E是△ABP的三条角平分线的交点.
∴点E是△ABP的内心.
(1)
∵PA,PB是⊙O的切线,
∴PA=PB,∠APO=∠BPO.
∴PO⊥AB.
∴∠AFP=90°.
∵BC为⊙O的直径,
∴∠BAC=90°.
∴∠BAC=∠AFP=90°.
∴AC//OP.
(2)连接BE.
∵PB是⊙O的切线,
∴∠PBO=90°.
∴∠PBE+∠OBE=90°.
∵PF⊥AB,
∴∠EBF+∠BEF=90°.
∵OB=OE,
∴∠BEF=∠OBE.
∴∠PBE=∠EBF.
∴BE平分∠PBF.
∵PA,PB是⊙O的切线,
∴PO平分∠APB.
∴点E是△ABP的三条角平分线的交点.
∴点E是△ABP的内心.
9. 新考向 数学文化 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示). 若直角三角形的内切圆半径为$3$,小正方形的面积为$49$,则大正方形的面积为
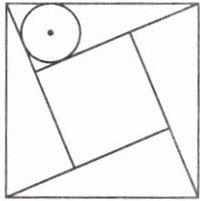
289
.
答案:
289
查看更多完整答案,请扫码查看


