《2025年名校课堂九年级数学上册人教版江西专版》

13. 新考向 跨学科 (2023·南昌二十八中期末)读一读下面的诗词：大江东去浪淘尽，千古风流数人物；而立之年督东吴，早逝英年两位数；十位恰小个位三，个位平方与寿同. 诗词大意是周瑜三十岁当上了东吴都督，去世时年龄是两位数，十位数比个位数小 $3$，个位数的平方等于他去世时的年龄. 若设他去世时年龄的个位数为 $x$，则根据题意可列出方程为$x^{2}=10(x-3)+x$.

答案： $x^{2}=10(x-3)+x$

14. 新考向 真实情境 (2023·南昌三中期中)去南昌了！国内最高的摩天轮去了！八一起义纪念馆去了！绳金塔去了！拌粉和瓦罐汤吃了！2023 年，南昌成为新晋“网红”旅游城市，今年南昌市某景点 6 月接待游客 5 万人，8 月接待游客 7.2 万人.
(1)求该景点接待游客 6 月至 8 月的月平均增长率.
(2)如果每月的增长率相同，预计 9 月接待游客的人数.

答案： 解:
(1)设该景点接待游客6月至8月的月平均增长率为$x$,由题意,得$5(1+x)^{2}=7.2$.解得$x_{1}=0.2=20\%$,$x_{2}=-2.2$(不符合题意,舍去).
答:该景点接待游客6月至8月的月平均增长率为20%.
(2)$7.2×(1+20\%)=8.64$(万人).
答:预计9月接待游客的人数为8.64万人.

15. (2024·上饶期中)如图，一个仓库的一边靠墙，另外三面用总长为 $32m$ 的木板材料围建，这堵墙的长为 $18m$，在与墙垂直的一边有一扇 $2m$ 宽的门，仓库面积为 $140m^{2}$.
(1)求这个仓库的宽和长.
(2)仓库存有一批商品，每件商品的进价为 15 元，销售单价为 25 元，平均每天能售出 80 件. 根据市场调查，销售单价每降低 $0.5$ 元，平均每天可多售出 20 件. 为了尽快减少库存，且实现平均每天 1280 元的利润，每件商品的定价应为多少元？

答案： 解:
(1)设这个仓库与墙垂直的边长为$x\ m$,则与墙平行的边长为$32+2-2x=(34-2x)\ m$.由题意,得$x(34-2x)=140$,解得$x_{1}=10$,$x_{2}=7$.当$x=7$时,$34-2x=20＞18$;当$x=10$时,$34-2x=14＜18$,$\therefore x=7$不合题意,舍去.$\therefore x=10$.$\therefore 34-2x=14$.
答:这个仓库的宽和长分别为10 m,14 m.
(2)设销售单价降低$x$元.根据题意,得$(25-15-x)(80+\frac{x}{0.5}× 20)=1280$.整理,得$x^{2}-8x+12=0$,解得$x_{1}=2$,$x_{2}=6$.$\because$要尽快减少库存,$\therefore x=6$.$\therefore$定价为$25-6=19$(元).
答:每件商品的定价应为19元.

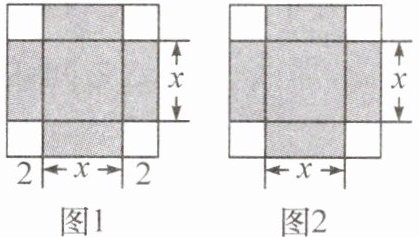
16. 新考向 数学文化 《代数学》中记载，形如 $x^{2}+8x = 33$ 的方程，求正数解的几何方法是：“如图 1，先构造一个面积为 $x^{2}$ 的正方形，再以正方形的边长为一边向外构造四个面积为 $2x$ 的矩形，得到大正方形的面积为 $33 + 16=49$，则该方程的正数解为 $7 - 4=3$.”小聪按此方法解关于 $x$ 的方程 $x^{2}+6x + m=0$ 时，构造出如图 2 所示的图形，已知阴影部分的面积为 19，则该方程的正数解为$2\sqrt{7}-3$.

答案： $2\sqrt{7}-3$